Sierpinski triangle
Last Updated :
20 Feb, 2023
Sierpinski triangle is a fractal and attractive fixed set with the overall shape of an equilateral triangle. It subdivides recursively into smaller triangles.
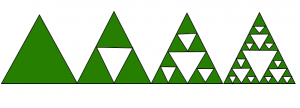
Examples :
Input : n = 4
Output :
*
* *
* *
* * * *
Input : n = 8
Output :
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
Approach :
Sierpinski Triangle will be constructed from an equilateral triangle by repeated removal of triangular subsets.
Steps for Construction :
1 . Take any equilateral triangle .
2 . Divide it into 4 smaller congruent triangle and remove the central triangle .
3 . Repeat step 2 for each of the remaining smaller triangles forever.
Below is the program to implement Sierpinski triangle
C++
#include <bits/stdc++.h>
using namespace std;
void printSierpinski(int n)
{
for (int y = n - 1; y >= 0; y--) {
for (int i = 0; i < y; i++) {
cout<<" ";
}
for (int x = 0; x + y < n; x++) {
if(x & y)
cout<<" "<<" ";
else
cout<<"* ";
}
cout<<endl;
}
}
int main()
{
int n = 16;
printSierpinski(n);
return 0;
}
|
Java
import java.util.*;
import java.io.*;
class GFG
{
static void printSierpinski(int n)
{
for (int y = n - 1; y >= 0; y--) {
for (int i = 0; i < y; i++) {
System.out.print(" ");
}
for (int x = 0; x + y < n; x++) {
if ((x & y) != 0)
System.out.print(" "
+ " ");
else
System.out.print("* ");
}
System.out.print("\n");
}
}
public static void main(String args[])
{
int n = 16;
printSierpinski(n);
}
}
|
Python3
def printSierpinski( n) :
y = n - 1
while(y >= 0) :
i = 0
while(i < y ):
print(" ",end="")
i = i + 1
x = 0
while(x + y < n ):
if ((x & y) != 0) :
print(" ", end = " ")
else :
print("* ", end = "")
x =x + 1
print()
y = y - 1
n = 16
printSierpinski(n)
|
C#
using System;
class GFG {
static void printSierpinski(int n)
{
for (int y = n - 1; y >= 0; y--) {
for (int i = 0; i < y; i++) {
Console.Write(" ");
}
for (int x = 0; x + y < n; x++) {
if ((x & y) != 0)
Console.Write(" " + " ");
else
Console.Write("* ");
}
Console.WriteLine();
}
}
public static void Main()
{
int n = 16;
printSierpinski(n);
}
}
|
PHP
<?php
function printSierpinski($n)
{
for ($y = $n - 1; $y >= 0; $y--)
{
for ($i = 0; $i < $y; $i++)
{
echo " ";
}
for ($x = 0; $x + $y < $n; $x++)
{
if($x & $y)
echo" ";
else
echo"* ";
}
echo "\n";
}
}
$n = 16;
printSierpinski($n);
?>
|
Javascript
<script>
function printSierpinski(n)
{
for (var y = n - 1; y >= 0; y--) {
for (var i = 0; i < y; i++) {
document.write(" ");
}
for (var x = 0; x + y < n; x++) {
if ((x & y) != 0)
document.write(" ");
else
document.write("* ");
}
document.write("<br>");
}
}
var n = 16;
printSierpinski(n);
</script>
|
Output :
*
* *
* *
* * * *
* *
* * * *
* * * *
* * * * * * * *
* *
* * * *
* * * *
* * * * * * * *
* * * *
* * * * * * * *
* * * * * * * *
* * * * * * * * * * * * * * * *
Time complexity: O(n2)
Auxiliary space: O(1)
References : Wiki
Share your thoughts in the comments
Please Login to comment...