Side of a regular n-sided polygon circumscribed in a circle
Last Updated :
24 Jun, 2022
Given two integers r and n where n is the number of sides of a regular polygon and r is the radius of the circle this polygon is circumscribed in. The task is to find the length of the side of polygon.

Examples:
Input: n = 5, r = 11
Output: 12.9256
Input: n = 3, r = 5
Output: 8.6576
Approach: Consider the image above and let angle AOB be theta then theta = 360 / n.
In right angled triangle 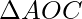 , angle ACO = 90 degrees and angle AOC = theta / 2.
, angle ACO = 90 degrees and angle AOC = theta / 2.
So, AC = OA * sin(theta / 2) = r * sin(theta / 2)
Therefore, side of the polygon, AB = 2 * AC i.e. 2 * r * sin(theta / 2).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float calculateSide(float n, float r)
{
float theta, theta_in_radians;
theta = 360 / n;
theta_in_radians = theta * 3.14 / 180;
return 2 * r * sin(theta_in_radians / 2);
}
int main()
{
float n = 3;
float r = 5;
cout << calculateSide(n, r);
}
|
Java
import java.lang.Math;
import java.io.*;
class GFG {
static double calculateSide(double n, double r)
{
double theta, theta_in_radians;
theta = 360 / n;
theta_in_radians = theta * 3.14 / 180;
return 2 * r * Math.sin(theta_in_radians / 2);
}
public static void main (String[] args) {
double n = 3;
double r = 5;
System.out.println (calculateSide(n, r));
}
}
|
Python3
from math import sin
def calculateSide(n, r):
theta = 360 / n
theta_in_radians = theta * 3.14 / 180
return 2 * r * sin(theta_in_radians / 2)
if __name__ == '__main__':
n = 3
r = 5
print('{0:.5}'.format(calculateSide(n, r)))
|
C#
using System;
class GFG {
static double calculateSide(double n, double r)
{
double theta, theta_in_radians;
theta = 360 / n;
theta_in_radians = theta * 3.14 / 180;
return Math.Round(2 * r * Math.Sin(theta_in_radians / 2),4);
}
public static void Main () {
double n = 3;
double r = 5;
Console.WriteLine(calculateSide(n, r));
}
}
|
PHP
<?php
function calculateSide($n, $r)
{
$theta; $theta_in_radians;
$theta = 360 / $n;
$theta_in_radians = $theta * 3.14 / 180;
return 2 * $r * sin($theta_in_radians / 2);
}
$n = 3;
$r = 5;
echo calculateSide($n, $r);
?>
|
Javascript
<script>
function calculateSide( n , r)
{
var theta, theta_in_radians;
theta = 360 / n;
theta_in_radians = theta * 3.14 / 180;
return 2 * r * Math.sin(theta_in_radians / 2);
}
var n = 3;
var r = 5;
document.write(calculateSide(n, r).toFixed(5));
</script>
|
Time Complexity: O(1), since there is no loop or recursion.
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...