Shortest path between two nodes in array like representation of binary tree
Last Updated :
12 Apr, 2022
Consider a binary tree in which each node has two children except the leaf nodes. If a node is labeled as ‘v’ then its right children will be labeled as 2v+1 and left children as 2v. Root is labelled as
Given two nodes labeled as i and j, the task is to find the shortest distance and the path from i to j. And print the path of node i and node j from root node.
Examples:
Input : i = 1, j = 2
Output : 1
Explanation:
Path is 1 2
Input: i = 4, j = 3
Output : 3
Explanation:
Path is 4 2 1 3
This problem is mainly an extension of Find distance between two given keys of a Binary Tree. Here we not only find the shortest distance but also the path.
The distance between the two nodes i and j will be equal to dist(i, LCA(i, j)) + dist(j, LCA(i, j)) where LCA means the lowest common ancestor of nodes labeled as i and j. If a number x is represented in the binary form then 2*x can be represented by appending 0 to the binary representation of x and 2x+1 can be represented by appending 1 to the binary representation of x. This is because when we append 0 all the terms present in the binary form of x shift left, so it gets doubled similarly when we append 1, we get 2x+1. Suppose the binary representation of a node is 1010 this tells us the path of this node from root. First-term ‘1’ represents root second term 0 represents left turn then the third term 1 represents a right turn from the previous node and finally, 0 represents the left turn.
Node 10 in binary form is 1010 and 13 in binary form is 1101 secondly length of the binary representation of any node also tells about its level in a binary tree. Suppose binary representation of i is m length and is 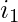 [Tex]i_2 [/Tex]…
[Tex]i_2 [/Tex]…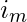 and binary representation of node j is n length
and binary representation of node j is n length 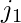 [Tex]j_2 [/Tex]……
[Tex]j_2 [/Tex]……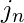 .
.
Thus we know the path of i and j from the root. Find out k such that for all p<=k 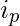 =
= 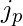 . This is the LCA of i and j in binary form.So dist(i, LCA(i, j)) will be m – k and dist(j, LCA(i, j)) = n – k. so answer will be m + n – 2k. And printing the path is also not a big issue just store the path of i to LCA and path of j to LCA and concatenate them.
. This is the LCA of i and j in binary form.So dist(i, LCA(i, j)) will be m – k and dist(j, LCA(i, j)) = n – k. so answer will be m + n – 2k. And printing the path is also not a big issue just store the path of i to LCA and path of j to LCA and concatenate them.
C++
#include <bits/stdc++.h>
using namespace std;
void ShortestPath(int i, int j, int k, int m, int n)
{
vector<int> path1, path2;
int x = m - 1;
path1.push_back(i);
while (x != k) {
path1.push_back(i / 2);
i = i / 2;
x--;
}
int y = n - 1;
path2.push_back(j);
while (y != k)
{
path2.push_back(j / 2);
j = j / 2;
y--;
}
for (int l = 0; l < path1.size(); l++)
cout << path1[l] << " ";
for (int l = path2.size() - 2; l >= 0; l--)
cout << path2[l] << " ";
cout << endl;
}
int ShortestDistance(int i, int j)
{
vector<int> v1, v2;
int p1 = i;
int p2 = j;
while (i != 0)
{
v1.push_back(i % 2);
i = i / 2;
}
while (j != 0) {
v2.push_back(j % 2);
j = j / 2;
}
reverse(v1.begin(), v1.end());
reverse(v2.begin(), v2.end());
int m = v1.size(), n = v2.size(), k = 0;
if (m < n)
{
while (k < m && v1[k] == v2[k])
k++;
}
else {
while (k < n && v1[k] == v2[k])
k++;
}
ShortestPath(p1, p2, k - 1, m, n);
return m + n - 2 * k;
}
int main()
{
cout << ShortestDistance(1, 2) << endl;
cout << ShortestDistance(4, 3) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static void ShortestPath(int i, int j, int k, int m,
int n)
{
Vector<Integer> path1=new Vector<Integer>(),
path2=new Vector<Integer>();
int x = m - 1;
path1.add(i);
while (x != k)
{
path1.add(i / 2);
i = i / 2;
x--;
}
int y = n - 1;
path2.add(j);
while (y != k)
{
path2.add(j / 2);
j = j / 2;
y--;
}
for (int l = 0; l < path1.size(); l++)
System.out.print( path1.get(l) + " ");
for (int l = path2.size() - 2; l >= 0; l--)
System.out.print( path2.get(l) + " ");
System.out.println();
}
static int ShortestDistance(int i, int j)
{
Vector<Integer> v1=new Vector<Integer>(),
v2=new Vector<Integer>();
int p1 = i;
int p2 = j;
while (i != 0)
{
v1.add(i % 2);
i = i / 2;
}
while (j != 0)
{
v2.add(j % 2);
j = j / 2;
}
Collections.reverse(v1);
Collections.reverse(v2);
int m = v1.size(), n = v2.size(), k = 0;
if (m < n)
{
while (k < m && v1.get(k) == v2.get(k))
k++;
}
else
{
while (k < n && v1.get(k) == v2.get(k))
k++;
}
ShortestPath(p1, p2, k - 1, m, n);
return m + n - 2 * k;
}
public static void main(String args[])
{
System.out.println( ShortestDistance(1, 2) );
System.out.println(ShortestDistance(4, 3) );
}
}
|
Python3
def ShortestPath(i, j, k, m, n):
path1, path2 = [], []
x = m - 1
path1.append(i)
while x != k:
path1.append(i // 2)
i = i // 2
x -= 1
y = n - 1
path2.append(j)
while y != k:
path2.append(j / 2)
j = j // 2
y -= 1
for l in range(0, len(path1)):
print(path1[l], end=" ")
for l in range(len(path2) - 2, -1, -1):
print(path2[l], end=" ")
print()
def ShortestDistance(i, j):
v1, v2 = [], []
p1, p2 = i, j
while i != 0:
v1.append(i % 2)
i = i // 2
while j != 0:
v2.append(j % 2)
j = j // 2
v1 = v1[::-1]
v2 = v2[::-1]
m, n, k = len(v1), len(v2), 0
if m < n:
while k < m and v1[k] == v2[k]:
k += 1
else:
while k < n and v1[k] == v2[k]:
k += 1
ShortestPath(p1, p2, k - 1, m, n)
return m + n - 2 * k
if __name__ == "__main__":
print(ShortestDistance(1, 2))
print(ShortestDistance(4, 3))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void ShortestPath(int i, int j, int k, int m,
int n)
{
List<int> path1=new List<int>(),
path2=new List<int>();
int x = m - 1;
path1.Add(i);
while (x != k)
{
path1.Add(i / 2);
i = i / 2;
x--;
}
int y = n - 1;
path2.Add(j);
while (y != k)
{
path2.Add(j / 2);
j = j / 2;
y--;
}
for (int l = 0; l < path1.Count; l++)
Console.Write( path1[l] + " ");
for (int l = path2.Count - 2; l >= 0; l--)
Console.Write( path2[l] + " ");
Console.WriteLine();
}
static int ShortestDistance(int i, int j)
{
List<int> v1=new List<int>(),
v2=new List<int>();
int p1 = i;
int p2 = j;
while (i != 0)
{
v1.Add(i % 2);
i = i / 2;
}
while (j != 0)
{
v2.Add(j % 2);
j = j / 2;
}
v1.Reverse();
v2.Reverse();
int m =v1.Count, n =v2.Count, k = 0;
if (m < n)
{
while (k < m && v1[k] == v2[k])
k++;
}
else
{
while (k < n && v1[k] == v2[k])
k++;
}
ShortestPath(p1, p2, k - 1, m, n);
return m + n - 2 * k;
}
public static void Main(String []args)
{
Console.WriteLine( ShortestDistance(1, 2) );
Console.WriteLine(ShortestDistance(4, 3) );
}
}
|
Javascript
<script>
function ShortestPath(i,j,k,m,n)
{
let path1=[];
let path2=[];
let x = m - 1;
path1.push(i);
while (x != k)
{
path1.push(Math.floor(i / 2));
i = Math.floor(i / 2);
x--;
}
let y = n - 1;
path2.push(j);
while (y != k)
{
path2.push(Math.floor(j / 2));
j = Math.floor(j / 2);
y--;
}
for (let l = 0; l < path1.length; l++)
document.write( path1[l] + " ");
for (let l = path2.length - 2; l >= 0; l--)
document.write( path2[l] + " ");
document.write("<br>");
}
function ShortestDistance(i,j)
{
let v1=[];
let v2=[];
let p1 = i;
let p2 = j;
while (i != 0)
{
v1.push(i % 2);
i = Math.floor(i / 2);
}
while (j != 0)
{
v2.push(j % 2);
j = Math.floor(j / 2);
}
v1.reverse();
v2.reverse();
let m =v1.length, n =v2.length, k = 0;
if (m < n)
{
while (k < m && v1[k] == v2[k])
k++;
}
else
{
while (k < n && v1[k] == v2[k])
k++;
}
ShortestPath(p1, p2, k - 1, m, n);
return m + n - 2 * k;
}
document.write( ShortestDistance(1, 2) +"<br>");
document.write(ShortestDistance(4, 3) +"<br>");
</script>
|
Output:
1 2
1
4 2 1 3
3
Complexity Analysis:
Time Complexity: O(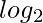 i +
i + 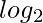 j) since we are shifting value of i and j to the right for every traversal
j) since we are shifting value of i and j to the right for every traversal
Auxiliary Space: O(log_2 i + log_2 j) since we are storing paths for every right shifting values of i and j.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...