Sequences and series have several important applications in several spheres of human activities. When sequences follow some specific patterns, they are usually called progressions. Arithmetic and Geometric progressions are some examples of commonly occurring progressions. Let’s see some problems on these progressions to understand them better.
Growth Patterns
Such types of number sequence problems first describe how a sequence of numbers is generated. Some terms of the sequence are given, and we need to figure out the patterns in them and then the next terms of the sequence.
Solving such sequences:
- Look for a pattern between the given numbers.
- Decide whether to use +, -, × or ÷
- Use the pattern to solve the sequence.
Increasing Pattern
Increasing Patterns as the name suggests will always be increasing in nature. The next term and the term just before that will all be similarly related with the help of operations (×, -, +).
Question: 6,13,27,55, ….. In the given sequence, what is the value of the next term?
Answer:
On looking carefully into the pattern, one can see that
13 = 6 × 2 + 1
27 = 13 × 2 + 1
55 = 27 × 2 + 1
This shows that every term is twice the preceding term plus one. So, let the next term be “a”.
a = 55 × 2 + 1
= 110 + 1
= 111
Hence, the next term is 111.
Decreasing Pattern
In decreasing Patterns, the next will be lesser than the previous term and two consecutive terms will follow a certain pattern.
Question: What is the next term in the series: 220,100,40, ….
Answer:
The series follow the pattern: 100 = (220×0.5)-10
40 = (100×0.5)-10
Therefore, the next term will be (40×0.5)-10 = 10
Arithmetic Progressions
In Arithmetic Progressions, the consecutive terms will have the same difference and are denoted as ‘d’, the first term is called as ‘a’, and the number of terms is denoted as ‘n’.
The formula for nth term is:
Tn= a+ (n-1)d
Question 1: 2, 5, 8, 11, …. Find the next term of the sequence.
Answer:
It can be noticed by carefully studying the terms of the sequence that the difference between each consecutive term remains the same. For example:
5 – 2 = 3
8 – 5 = 3
11 – 8 = 3
So, the next will be at a difference of three from the last term. Since the last term of the sequence is 11. The next terms will be 14.
OR
The formula for nth term in Arithmetic progression can also be used here, 5th term is required here:
a = 2
d = (3)
T5 = 2+(5-1)(3)
= 2+12
= 14
Question 2: 15, 12, 9, … __. Find the next term.
Answer:
In this problem also, all the terms have a difference of three between them. The difference is that the sequence in decreasing in nature. Since the last term is 9, the next term will be 3 less than the last term. So, the last term will be 6.
Fibonacci Sequence
Sometimes there are sequences for which pattern is not visible, the Fibonacci sequence is an example of such a sequence. It is a very commonly occurring sequence in the field of mathematics and computer science.
The number is arranged as, 1, 1, 2, 3, 5, 8 …. Here the pattern is not visible, this sequence proceeds in a manner that depends on its history.
Let an be the nth term for the sequence. In this sequence an = an-1 + an-2.
For example,
a2 = a1 + a0 i.e 2 = 1 + 1,
a3 = a1 + a2 i.e 3 = 2 + 1,
a4 = a3 + a2 i.e 5 = 2 + 3 and,
a5 = a4 + a3 i.e 8 = 5 + 3.
Question: What is the next term in the Fibonacci series: 1,1,2,3,5,8,13,……
Answer:
In Fibonacci Series, the next term is the sum of the last two terms.
Therefore, the next term will be (8+13)= 21
Geometric Series
Before starting out with the problems related to a geometric progression. Let’s take a quick recap of the formulas for the sum and nth term of a GP.
The general form of a geometric progression is a, ar, ar2, ar3 …… where a = first term, r = common ratio and an be the nth term.
- The nth term of the progression: an = arn-1.
- Sum of n-terms of GP:
![Rendered by QuickLaTeX.com S_{n} = a[\frac{r^{n}-1}{r-1}] \text{ where } r \ne 1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26d7a43f5352fab7c4b8a0c41026928d_l3.png)
- Sum of infinite GP:
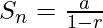
Finite GP problems
These kinds of problems include the geometric series where there are a finite number of terms.
Question 1: The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of the 2nd hour, 4th hour, and nth hour?
Answer:
The growth of the bacteria makes a GP, 30, 60, 120,….. and so on.
In this GP, a = 30, r = 2. Let the number of bacteria at nth hour be an.
At n = 2, a2 = ar2-1
= (30)(2)2-1 = 30 × 2 = 60
At n = 4, a4 = ar4-1
= (30)(2)4-1 = 30 × 23 = 240
At nth step an = ar(n-1) = 30 × 2n-1
Question 2: A person has 2 parents, 4 grandparents, 8 great-grandparents, and so on. Find the number of his ancestors during the ten generations preceding his own.
Answer:
This is a problem of finite GP. The sequence can be thought like this,
2, 4, 8, 16, …..
So, the total number of ancestors in 10 generation of his family.
2, 4, 8, 16, 32, …..10 terms.
Here, a = 2, r = 2 and n = 10
S10 = a ![Rendered by QuickLaTeX.com S_{n} = a[\frac{r^{n}-1}{r-1}] \\ = 2[\frac{2^{10} - 1}{2 - 1}] \\ = 2[1023] = 2046](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e45f86159ca0c5e1a0e8da835da5c9c_l3.png)
Infinite GP Problems
An infinite geometric series is the sum of an infinite geometric sequence. This series would have no last term
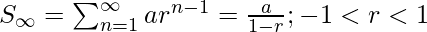
Question 1: A monkey is swinging from a tree. On the first swing, she passes through an arc of 24m. With each swing, she passes through an arc of 24m. With each swing, she passes through an arc half the length of the previous swing. What is the total distance traveled by the monkey when she completes her 100000th swing?
Answer:
Now this movement represents a GP with a = 24 and r = 1/2. Now, since the GP is decreasing and the question asks for the sum till 100000th term. To save the calculation , we can consider it an infinite GP and round of the answer we get.
Sum of an infinite GP = 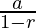
Here, a = 24 and r = 1/2. Let the sum be S
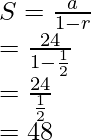
So the monkey travels almost 24m in these many swings.
Question 2: A ball was dropped from a 24-inch high table. The ball rebounds and always reaches three fourth of the distance fallen. What is the approximate distance the ball travels before finally coming at rest on the ground.
Answer:
It should be noticed that this problem actually involves two infinite geometric series. The first series involves ball falling and the other series involves ball rising after rebounding from the ground.
Falling: a1 = 24 , r = 3/4
Rising: a2 = 24(3/4) = 18 ,r = 3/4
Using the formula for infinite geometric series,
S = 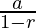
Let S be the total distance travelled:
S = Srising + Sfalling
Srising =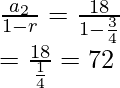
Sfalling = 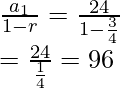
Now, S = Srising + Sfalling = 72 + 96 = 168
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...