Sequence Alignment problem
Last Updated :
22 Feb, 2023
Given as an input two strings, 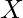 =
= 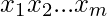 , and
, and 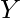 =
= 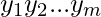 , output the alignment of the strings, character by character, so that the net penalty is minimized. The penalty is calculated as:
, output the alignment of the strings, character by character, so that the net penalty is minimized. The penalty is calculated as:
- A penalty of
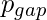 occurs if a gap is inserted between the string.
occurs if a gap is inserted between the string. - A penalty of
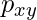 occurs for mis-matching the characters of
occurs for mis-matching the characters of 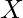 and
and 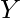 .
.
Examples:
Input : X = CG, Y = CA, p_gap = 3, p_xy = 7
Output : X = CG_, Y = C_A, Total penalty = 6
Input : X = AGGGCT, Y = AGGCA, p_gap = 3, p_xy = 2
Output : X = AGGGCT, Y = A_GGCA, Total penalty = 5
Input : X = CG, Y = CA, p_gap = 3, p_xy = 5
Output : X = CG, Y = CA, Total penalty = 5
A brief Note on the history of the problem
The Sequence Alignment problem is one of the fundamental problems of Biological Sciences, aimed at finding the similarity of two amino-acid sequences. Comparing amino-acids is of prime importance to humans, since it gives vital information on evolution and development. Saul B. Needleman and Christian D. Wunsch devised a dynamic programming algorithm to the problem and got it published in 1970. Since then, numerous improvements have been made to improve the time complexity and space complexity, however these are beyond the scope of discussion in this post.
Solution: We can use dynamic programming to solve this problem. The feasible solution is to introduce gaps into the strings, so as to equalise the lengths. Since it can be easily proved that the addition of extra gaps after equalising the lengths will only lead to increment of penalty.
Optimal Substructure:
It can be observed from an optimal solution, for example from the given sample input, that the optimal solution narrows down to only three candidates.
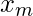 and
and 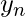 .
. 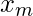 and gap.
and gap. - gap and
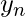 .
.
Proof of Optimal Substructure.
We can easily prove by contradiction. Let 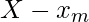 be
be 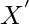 and
and 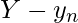 be
be 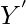 . Suppose that the induced alignment of
. Suppose that the induced alignment of 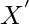 ,
, 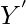 has some penalty
has some penalty 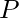 , and a competitor alignment has a penalty
, and a competitor alignment has a penalty 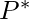 , with
, with  .
.
Now, appending 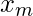 and
and 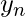 , we get an alignment with penalty
, we get an alignment with penalty 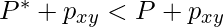 . This contradicts the optimality of the original alignment of
. This contradicts the optimality of the original alignment of 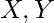 .
.
Hence, proved.
Let ![Rendered by QuickLaTeX.com dp[i][j]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-023956199cecb2c76d2090e129a2591e_l3.png) be the penalty of the optimal alignment of
be the penalty of the optimal alignment of 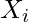 and
and 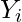 . Then, from the optimal substructure,
. Then, from the optimal substructure, ![Rendered by QuickLaTeX.com dp[i][j] = min(dp[i-1][j-1] + p_{xy}, dp[i-1][j] + p_{gap}, dp[i][j-1] + p_{gap})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c047761f6c12b914c615db5411e10953_l3.png) .
.
The total minimum penalty is thus, ![Rendered by QuickLaTeX.com dp[m][n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-70e55c7df0a10e2a77e550b755b80442_l3.png) .
.
Reconstructing the solution
To Reconstruct,
- Trace back through the filled table, starting
![Rendered by QuickLaTeX.com dp[m][n]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-70e55c7df0a10e2a77e550b755b80442_l3.png) .
. - When
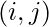
- if it was filled using case 1, go to
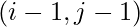 .
. - if it was filled using case 2, go to
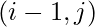 .
. - if it was filled using case 3, go to
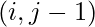 .
.
- if either i = 0 or j = 0, match the remaining substring with gaps.
Below is the implementation of the above solution.
C++
#include <bits/stdc++.h>
using namespace std;
void getMinimumPenalty(string x, string y, int pxy, int pgap)
{
int i, j;
int m = x.length();
int n = y.length();
int dp[n+m+1][n+m+1] = {0};
for (i = 0; i <= (n+m); i++)
{
dp[i][0] = i * pgap;
dp[0][i] = i * pgap;
}
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
if (x[i - 1] == y[j - 1])
{
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = min({dp[i - 1][j - 1] + pxy ,
dp[i - 1][j] + pgap ,
dp[i][j - 1] + pgap });
}
}
}
int l = n + m;
i = m; j = n;
int xpos = l;
int ypos = l;
int xans[l+1], yans[l+1];
while ( !(i == 0 || j == 0))
{
if (x[i - 1] == y[j - 1])
{
xans[xpos--] = (int)x[i - 1];
yans[ypos--] = (int)y[j - 1];
i--; j--;
}
else if (dp[i - 1][j - 1] + pxy == dp[i][j])
{
xans[xpos--] = (int)x[i - 1];
yans[ypos--] = (int)y[j - 1];
i--; j--;
}
else if (dp[i - 1][j] + pgap == dp[i][j])
{
xans[xpos--] = (int)x[i - 1];
yans[ypos--] = (int)'_';
i--;
}
else if (dp[i][j - 1] + pgap == dp[i][j])
{
xans[xpos--] = (int)'_';
yans[ypos--] = (int)y[j - 1];
j--;
}
}
while (xpos > 0)
{
if (i > 0) xans[xpos--] = (int)x[--i];
else xans[xpos--] = (int)'_';
}
while (ypos > 0)
{
if (j > 0) yans[ypos--] = (int)y[--j];
else yans[ypos--] = (int)'_';
}
int id = 1;
for (i = l; i >= 1; i--)
{
if ((char)yans[i] == '_' && (char)xans[i] == '_')
{
id = i + 1;
break;
}
}
cout << "Minimum Penalty in aligning the genes = ";
cout << dp[m][n] << "\n";
cout << "The aligned genes are :\n";
for (i = id; i <= l; i++)
{
cout<<(char)xans[i];
}
cout << "\n";
for (i = id; i <= l; i++)
{
cout << (char)yans[i];
}
return;
}
int main(){
string gene1 = "AGGGCT";
string gene2 = "AGGCA";
int misMatchPenalty = 3;
int gapPenalty = 2;
getMinimumPenalty(gene1, gene2,
misMatchPenalty, gapPenalty);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
import java.lang.*;
class GFG
{
static void getMinimumPenalty(String x, String y,
int pxy, int pgap)
{
int i, j;
int m = x.length();
int n = y.length();
int dp[][] = new int[n + m + 1][n + m + 1];
for (int[] x1 : dp)
Arrays.fill(x1, 0);
for (i = 0; i <= (n + m); i++)
{
dp[i][0] = i * pgap;
dp[0][i] = i * pgap;
}
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
if (x.charAt(i - 1) == y.charAt(j - 1))
{
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1] + pxy ,
dp[i - 1][j] + pgap) ,
dp[i][j - 1] + pgap );
}
}
}
int l = n + m;
i = m; j = n;
int xpos = l;
int ypos = l;
int xans[] = new int[l + 1];
int yans[] = new int[l + 1];
while ( !(i == 0 || j == 0))
{
if (x.charAt(i - 1) == y.charAt(j - 1))
{
xans[xpos--] = (int)x.charAt(i - 1);
yans[ypos--] = (int)y.charAt(j - 1);
i--; j--;
}
else if (dp[i - 1][j - 1] + pxy == dp[i][j])
{
xans[xpos--] = (int)x.charAt(i - 1);
yans[ypos--] = (int)y.charAt(j - 1);
i--; j--;
}
else if (dp[i - 1][j] + pgap == dp[i][j])
{
xans[xpos--] = (int)x.charAt(i - 1);
yans[ypos--] = (int)'_';
i--;
}
else if (dp[i][j - 1] + pgap == dp[i][j])
{
xans[xpos--] = (int)'_';
yans[ypos--] = (int)y.charAt(j - 1);
j--;
}
}
while (xpos > 0)
{
if (i > 0) xans[xpos--] = (int)x.charAt(--i);
else xans[xpos--] = (int)'_';
}
while (ypos > 0)
{
if (j > 0) yans[ypos--] = (int)y.charAt(--j);
else yans[ypos--] = (int)'_';
}
int id = 1;
for (i = l; i >= 1; i--)
{
if ((char)yans[i] == '_' &&
(char)xans[i] == '_')
{
id = i + 1;
break;
}
}
System.out.print("Minimum Penalty in " +
"aligning the genes = ");
System.out.print(dp[m][n] + "\n");
System.out.println("The aligned genes are :");
for (i = id; i <= l; i++)
{
System.out.print((char)xans[i]);
}
System.out.print("\n");
for (i = id; i <= l; i++)
{
System.out.print((char)yans[i]);
}
return;
}
public static void main(String[] args)
{
String gene1 = "AGGGCT";
String gene2 = "AGGCA";
int misMatchPenalty = 3;
int gapPenalty = 2;
getMinimumPenalty(gene1, gene2,
misMatchPenalty, gapPenalty);
}
}
|
Python3
import numpy as np
def get_minimum_penalty(x:str, y:str, pxy:int, pgap:int):
i = 0
j = 0
m = len(x)
n = len(y)
dp = np.zeros([m+1,n+1], dtype=int)
dp[0:(m+1),0] = [ i * pgap for i in range(m+1)]
dp[0,0:(n+1)] = [ i * pgap for i in range(n+1)]
i = 1
while i <= m:
j = 1
while j <= n:
if x[i - 1] == y[j - 1]:
dp[i][j] = dp[i - 1][j - 1]
else:
dp[i][j] = min(dp[i - 1][j - 1] + pxy,
dp[i - 1][j] + pgap,
dp[i][j - 1] + pgap)
j += 1
i += 1
l = n + m
i = m
j = n
xpos = l
ypos = l
xans = np.zeros(l+1, dtype=int)
yans = np.zeros(l+1, dtype=int)
while not (i == 0 or j == 0):
if x[i - 1] == y[j - 1]:
xans[xpos] = ord(x[i - 1])
yans[ypos] = ord(y[j - 1])
xpos -= 1
ypos -= 1
i -= 1
j -= 1
elif (dp[i - 1][j - 1] + pxy) == dp[i][j]:
xans[xpos] = ord(x[i - 1])
yans[ypos] = ord(y[j - 1])
xpos -= 1
ypos -= 1
i -= 1
j -= 1
elif (dp[i - 1][j] + pgap) == dp[i][j]:
xans[xpos] = ord(x[i - 1])
yans[ypos] = ord('_')
xpos -= 1
ypos -= 1
i -= 1
elif (dp[i][j - 1] + pgap) == dp[i][j]:
xans[xpos] = ord('_')
yans[ypos] = ord(y[j - 1])
xpos -= 1
ypos -= 1
j -= 1
while xpos > 0:
if i > 0:
i -= 1
xans[xpos] = ord(x[i])
xpos -= 1
else:
xans[xpos] = ord('_')
xpos -= 1
while ypos > 0:
if j > 0:
j -= 1
yans[ypos] = ord(y[j])
ypos -= 1
else:
yans[ypos] = ord('_')
ypos -= 1
id = 1
i = l
while i >= 1:
if (chr(yans[i]) == '_') and chr(xans[i]) == '_':
id = i + 1
break
i -= 1
print(f"Minimum Penalty in aligning the genes = {dp[m][n]}")
print("The aligned genes are:")
i = id
x_seq = ""
while i <= l:
x_seq += chr(xans[i])
i += 1
print(f"X seq: {x_seq}")
i = id
y_seq = ""
while i <= l:
y_seq += chr(yans[i])
i += 1
print(f"Y seq: {y_seq}")
def test_get_minimum_penalty():
gene1 = "AGGGCT"
gene2 = "AGGCA"
mismatch_penalty = 3
gap_penalty = 2
get_minimum_penalty(gene1, gene2, mismatch_penalty, gap_penalty)
test_get_minimum_penalty()
|
C#
using System;
class GFG
{
public static void getMinimumPenalty(string x, string y, int pxy, int pgap)
{
int i, j;
int m = x.Length;
int n = y.Length;
int[,] dp = new int[n+m+1,n+m+1];
for(int q = 0; q < n+m+1; q++)
for(int w = 0; w < n+m+1; w++)
dp[q,w] = 0;
for (i = 0; i <= (n+m); i++)
{
dp[i,0] = i * pgap;
dp[0,i] = i * pgap;
}
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
if (x[i - 1] == y[j - 1])
{
dp[i,j] = dp[i - 1,j - 1];
}
else
{
dp[i,j] = Math.Min(Math.Min(dp[i - 1,j - 1] + pxy ,
dp[i - 1,j] + pgap) ,
dp[i,j - 1] + pgap );
}
}
}
int l = n + m;
i = m; j = n;
int xpos = l;
int ypos = l;
int[] xans = new int[l+1];
int [] yans = new int[l+1];
while ( !(i == 0 || j == 0))
{
if (x[i - 1] == y[j - 1])
{
xans[xpos--] = (int)x[i - 1];
yans[ypos--] = (int)y[j - 1];
i--; j--;
}
else if (dp[i - 1,j - 1] + pxy == dp[i,j])
{
xans[xpos--] = (int)x[i - 1];
yans[ypos--] = (int)y[j - 1];
i--; j--;
}
else if (dp[i - 1,j] + pgap == dp[i,j])
{
xans[xpos--] = (int)x[i - 1];
yans[ypos--] = (int)'_';
i--;
}
else if (dp[i,j - 1] + pgap == dp[i,j])
{
xans[xpos--] = (int)'_';
yans[ypos--] = (int)y[j - 1];
j--;
}
}
while (xpos > 0)
{
if (i > 0) xans[xpos--] = (int)x[--i];
else xans[xpos--] = (int)'_';
}
while (ypos > 0)
{
if (j > 0) yans[ypos--] = (int)y[--j];
else yans[ypos--] = (int)'_';
}
int id = 1;
for (i = l; i >= 1; i--)
{
if ((char)yans[i] == '_' && (char)xans[i] == '_')
{
id = i + 1;
break;
}
}
Console.Write("Minimum Penalty in aligning the genes = " + dp[m,n] + "\n");
Console.Write("The aligned genes are :\n");
for (i = id; i <= l; i++)
{
Console.Write((char)xans[i]);
}
Console.Write("\n");
for (i = id; i <= l; i++)
{
Console.Write((char)yans[i]);
}
return;
}
static void Main()
{
string gene1 = "AGGGCT";
string gene2 = "AGGCA";
int misMatchPenalty = 3;
int gapPenalty = 2;
getMinimumPenalty(gene1, gene2,
misMatchPenalty, gapPenalty);
}
}
|
PHP
<?php
function getMinimumPenalty($x, $y,
$pxy, $pgap)
{
$i; $j;
$m = strlen($x);
$n = strlen($y);
$dp[$n + $m + 1][$n + $m + 1] = array(0);
for ($i = 0; $i <= ($n+$m); $i++)
{
$dp[$i][0] = $i * $pgap;
$dp[0][$i] = $i * $pgap;
}
for ($i = 1; $i <= $m; $i++)
{
for ($j = 1; $j <= $n; $j++)
{
if ($x[$i - 1] == $y[$j - 1])
{
$dp[$i][$j] = $dp[$i - 1][$j - 1];
}
else
{
$dp[$i][$j] = min($dp[$i - 1][$j - 1] + $pxy ,
$dp[$i - 1][$j] + $pgap ,
$dp[$i][$j - 1] + $pgap );
}
}
}
$l = $n + $m;
$i = $m; $j = $n;
$xpos = $l;
$ypos = $l;
while ( !($i == 0 || $j == 0))
{
if ($x[$i - 1] == $y[$j - 1])
{
$xans[$xpos--] = $x[$i - 1];
$yans[$ypos--] = $y[$j - 1];
$i--; $j--;
}
else if ($dp[$i - 1][$j - 1] +
$pxy == $dp[$i][$j])
{
$xans[$xpos--] = $x[$i - 1];
$yans[$ypos--] = $y[$j - 1];
$i--; $j--;
}
else if ($dp[$i - 1][$j] +
$pgap == $dp[$i][$j])
{
$xans[$xpos--] = $x[$i - 1];
$yans[$ypos--] = '_';
$i--;
}
else if ($dp[$i][$j - 1] +
$pgap == $dp[$i][$j])
{
$xans[$xpos--] = '_';
$yans[$ypos--] = $y[$j - 1];
$j--;
}
}
while ($xpos > 0)
{
if ($i > 0) $xans[$xpos--] = $x[--$i];
else $xans[$xpos--] = '_';
}
while ($ypos > 0)
{
if ($j > 0)
$yans[$ypos--] = $y[--$j];
else
$yans[$ypos--] = '_';
}
$id = 1;
for ($i = $l; $i >= 1; $i--)
{
if ($yans[$i] == '_' &&
$xans[$i] == '_')
{
$id = $i + 1;
break;
}
}
echo "Minimum Penalty in ".
"aligning the genes = ";
echo $dp[$m][$n] . "\n";
echo "The aligned genes are :\n";
for ($i = $id; $i <= $l; $i++)
{
echo $xans[$i];
}
echo "\n";
for ($i = $id; $i <= $l; $i++)
{
echo $yans[$i];
}
return;
}
$gene1 = "AGGGCT";
$gene2 = "AGGCA";
$misMatchPenalty = 3;
$gapPenalty = 2;
getMinimumPenalty($gene1, $gene2,
$misMatchPenalty, $gapPenalty);
?>
|
Javascript
function getMinimumPenalty(x, y, pxy, pgap) {
let i, j;
let m = x.length;
let n = y.length;
let dp = new Array(n + m + 1).fill().map(() => new Array(n + m + 1).fill(0));
for (i = 0; i <= (n + m); i++)
{
dp[i][0] = i * pgap;
dp[0][i] = i * pgap;
}
for (i = 1; i <= m; i++)
{
for (j = 1; j <= n; j++)
{
if (x.charAt(i - 1) == y.charAt(j - 1))
{
dp[i][j] = dp[i - 1][j - 1];
}
else
{
dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1] + pxy ,
dp[i - 1][j] + pgap) ,
dp[i][j - 1] + pgap );
}
}
}
let l = n + m;
i = m; j = n;
let xpos = l;
let ypos = l;
let xans = new Array(l + 1);
let yans = new Array(l + 1);
while ( !(i == 0 || j == 0))
{
if (x.charAt(i - 1) == y.charAt(j - 1))
{
xans[xpos--] = x.charCodeAt(i - 1);
yans[ypos--] = y.charCodeAt(j - 1);
i--; j--;
}
else if (dp[i - 1][j - 1] + pxy == dp[i][j])
{
xans[xpos--] = x.charCodeAt(i - 1);
yans[ypos--] = '_'.charCodeAt(0);
i--; j--;
}
else if (dp[i - 1][j] + pgap == dp[i][j])
{
xans[xpos--] = x.charCodeAt(i - 1);
yans[ypos--] = '_'.charCodeAt(0);
i--;
}
else if (dp[i][j - 1] + pgap == dp[i][j])
{
xans[xpos--] = '_'.charCodeAt(0);
yans[ypos--] = y.charCodeAt(j - 1);
j--;
}
}
while (xpos > 0)
{
if (i > 0) xans[xpos--] = x.charCodeAt(--i);
else xans[xpos--] = '_'.charCodeAt(0);
}
while (ypos > 0)
{
if (j > 0) yans[ypos--] = y.charCodeAt(--j);
else yans[ypos--] = '_'.charCodeAt(0);
}
let id = 1;
for (i = l; i >= 1; i--)
{
if (String.fromCharCode(yans[i]) == '_' &&
String.fromCharCode(xans[i]) == '_')
{
id = i + 1;
break;
}
}
console.log("Minimum Penalty in " +
"aligning the genes = " + dp[m][n]);
console.log("The aligned genes are :");
let temp="";
for (i = id; i <= l; i++)
{
temp=temp+String.fromCharCode(xans[i]);
}
console.log(temp);
temp="";
for (i = id; i <= l-1; i++)
{
temp=temp+String.fromCharCode(yans[i]);
}
console.log(temp+"A");
return;
}
function main() {
let gene1 = "AGGGCT";
let gene2 = "AGGCA";
let misMatchPenalty = 3;
let gapPenalty = 2;
getMinimumPenalty(gene1, gene2,
misMatchPenalty, gapPenalty);
}
main();
|
OutputMinimum Penalty in aligning the genes = 5
The aligned genes are :
AGGGCT
A_GGCA
Complexity Analysis:
- Time Complexity :
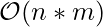
- Space Complexity :
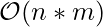
Share your thoughts in the comments
Please Login to comment...