Selection Sort VS Bubble Sort
Last Updated :
29 Jan, 2023
Not a valid contributionIn this, we will cover the comparison between Selection Sort VS Bubble Sort. The resources required by Selection Sort & Bubble Sort algorithms on the basis of Time and Space Complexity are as follows.
Time Complexity - 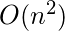 Space Complexity -
Space Complexity - 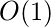
Let’s dive deep into the working of these algorithms.
Selection Sort :
The selection sort algorithm generally is the first sorting algorithm that is taught to us. Here in every iteration of the inner loop, the smallest element is replaced with the starting element in each loop. After the end of each loop, we increment the starting position by 1 and run it till the second last element in the array. Hence, by doing so at the end of the outer loop we will be having a sorted array.
The image below explains the iteration of Selection Sort Algorithm.
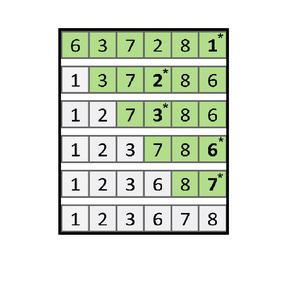
Here we can simplify the selection sort algorithm by saying that the sorting here is done on the basis of the smallest to the largest element. The smallest element is first sorted and then the second smallest element and so on.
Implementation of Selection Sort :
Below is the implementation of the above-explained algorithm.
C++
#include <iostream>
using namespace std;
void Selection_Sort(int arr[], int n)
{
for(int i = 0; i < n - 1; ++i)
{
int min_index = i;
for(int j = i + 1; j < n; ++j)
{
if(arr[j] < arr[min_index])
min_index = j;
}
swap(arr[i], arr[min_index]);
}
}
int main()
{
int n = 5;
int arr[5] = {2, 0, 1, 4, 3};
Selection_Sort(arr, n);
cout<<"The Sorted Array by using Selection Sort is : ";
for(int i = 0; i < n; ++i)
cout<<arr[i]<<" ";
return 0;
}
|
Java
class GFG{
static void Selection_Sort(int arr[], int n)
{
for(int i = 0; i < n - 1; ++i)
{
int min_index = i;
for(int j = i + 1; j < n; ++j)
{
if(arr[j] < arr[min_index])
min_index = j;
}
int temp = arr[i];
arr[i] = arr[min_index];
arr[min_index] = temp;
}
}
public static void main(String[] args)
{
int n = 5;
int arr[] = {2, 0, 1, 4, 3};
Selection_Sort(arr, n);
System.out.print("The Sorted Array by using Selection Sort is : ");
for(int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
}
}
|
Python3
def Selection_Sort(arr, n):
for i in range(n - 1):
min_index = i
for j in range(i + 1, n):
if (arr[j] < arr[min_index]):
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
n = 5
arr = [ 2, 0, 1, 4, 3 ]
Selection_Sort(arr, n)
print("The Sorted Array by using " \
"Selection Sort is : ", end = '')
for i in range(n):
print(arr[i], end = " ")
|
C#
using System;
public class GFG{
static void Selection_Sort(int []arr, int n)
{
for(int i = 0; i < n - 1; ++i)
{
int min_index = i;
for(int j = i + 1; j < n; ++j)
{
if(arr[j] < arr[min_index])
min_index = j;
}
int temp = arr[i];
arr[i] = arr[min_index];
arr[min_index] = temp;
}
}
public static void Main(String[] args)
{
int n = 5;
int []arr = {2, 0, 1, 4, 3};
Selection_Sort(arr, n);
Console.Write("The Sorted Array by using Selection Sort is : ");
for(int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
}
}
|
Javascript
<script>
function Selection_Sort(arr, n)
{
for(let i = 0; i < n - 1; ++i)
{
let min_index = i;
for(let j = i + 1; j < n; ++j)
{
if(arr[j] < arr[min_index])
min_index = j;
}
let temp = arr[i];
arr[i] = arr[min_index];
arr[min_index] = temp;
}
}
let n = 5;
let arr = [2, 0, 1, 4, 3];
Selection_Sort(arr, n);
document.write("The Sorted Array by using Selection Sort is : ");
for(let i = 0; i < n; ++i)
document.write(arr[i] + " ");
</script>
|
OutputThe Sorted Array by using Selection Sort is : 0 1 2 3 4
Bubble Sort :
The bubble sort algorithm might look a little bit confusing when we first study it. But here is the easy explanation of it. Here swapping is carried on in two ways. In every iteration of the outer loop, the largest element is found and swapped with the last element in the loop. In the inner loop, we do pairwise swapping of two consecutive elements. In every inner loop, we go from the first element to the one less element we went in the previous loop. The image below shows the 1st iteration of the inner loop in the Bubble Sort Algorithm.
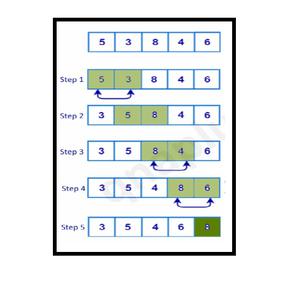
Here we can simplify the bubble sort algorithm by saying that the sorting here is done on the basis of the largest to the smallest element. The largest element is first kept in the last location in the array. Then the second largest element in the second last location as so on.
Implementation of Bubble Sort :
Below is the implementation of the above-explained algorithm.
C++
#include <iostream>
using namespace std;
void Bubble_Sort(int arr[], int n)
{
for(int i = 1; i < n; ++i)
{
for(int j = 0; j <= (n - i - 1); ++j)
{
if(arr[j] > arr[j + 1])
swap(arr[j], arr[j + 1]);
}
}
}
int main()
{
int n = 5;
int arr[5] = {2, 0, 1, 4, 3};
Bubble_Sort(arr, n);
cout<<"The Sorted Array by using Bubble Sort is : ";
for(int i = 0; i < n; ++i)
cout<<arr[i]<<" ";
return 0;
}
|
Java
import java.io.*;
class GFG{
static void Bubble_Sort(int arr[], int n)
{
for(int i = 1; i < n; ++i)
{
for(int j = 0; j <= (n - i - 1); ++j)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
public static void main(String[] args)
{
int n = 5;
int arr[] = { 2, 0, 1, 4, 3 };
Bubble_Sort(arr, n);
System.out.print("The Sorted Array by using Bubble Sort is : ");
for(int i = 0; i < n; ++i)
System.out.print(arr[i]+" ");
}
}
|
Python3
def Bubble_Sort(arr, n):
for i in range(1, n):
for j in range(0, n - i):
if (arr[j] > arr[j + 1]):
arr[j], arr[j + 1] = arr[j + 1], arr[j]
return arr
n = 5
arr = [ 2, 0, 1, 4, 3 ]
arr = Bubble_Sort(arr, n)
print("The Sorted Array by using Bubble Sort is : ", end = '')
for i in range(n):
print(arr[i], end = " ")
|
C#
using System;
public class GFG{
static void Bubble_Sort(int[] arr, int n)
{
for(int i = 1; i < n; ++i)
{
for(int j = 0; j <= (n - i - 1); ++j)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
static public void Main ()
{
int n = 5;
int[] arr = { 2, 0, 1, 4, 3 };
Bubble_Sort(arr, n);
Console.Write("The Sorted Array by using Bubble Sort is : ");
for(int i = 0; i < n; ++i){
Console.Write(arr[i]+" ");
}
}
}
|
Javascript
<script>
function Bubble_Sort( arr, n)
{
for(var i = 1; i < n; ++i)
{
for(var j = 0; j <= (n - i - 1); ++j)
{
if(arr[j] > arr[j + 1]){
var temm = arr[j];
arr[j] = arr[j + 1];
arr[j+1] = temm;
}
}
}
}
var n = 5;
var arr = [2, 0, 1, 4, 3];
Bubble_Sort(arr, n);
document.write("The Sorted Array by using Bubble Sort is : ");
for(var i = 0; i < n; i++){
document.write(arr[i]+" ");
}
</script>
|
OutputThe Sorted Array by using Bubble Sort is : 0 1 2 3 4
Adding Intelligence To Bubble Sort:
- We must account for the fact that even if our data is in sorted form initially, our current algorithm will perform all the iterations.
- As shown by above code, we swap two elements (say i and i+1) when arr[i] > arr[i+1]. Therefore, even if our data is sorted already (or is sorted just after few iterations) our algorithm will still run,
- However, we can tweak our code so that our algorithm recognizes when given data is sorted and no further iterations are required.
- We can achieve this by simply adding a “flag” variable. Initialize this “flag” variable to false outside inner loop and set it to true if at any point ( arr[j] > arr[j+1] ) condition is true.
- After inner loop is exited, check flag. If flag == true i.e, it was changed and swap operation was carried out. However, if flag == false, it means that no swap was carried out for entire iteration and hence our data is now sorted and no further iterations are required.
C++
#include <iostream>
using namespace std;
void Bubble_Sort(int arr[], int n)
{
bool flag;
for (int i = 1; i < n; ++i) {
flag = false;
for (int j = 0; j <= (n - i - 1); ++j) {
if (arr[j] > arr[j + 1]) {
swap(arr[j], arr[j + 1]);
flag = true;
}
}
if (flag == false)
break;
}
}
int main()
{
int n = 5;
int arr[5] = { 2, 0, 1, 4, 3 };
Bubble_Sort(arr, n);
cout << "The Sorted Array by using Bubble Sort is : ";
for (int i = 0; i < n; ++i)
cout << arr[i] << " ";
return 0;
}
|
Java
import java.io.*;
class GFG{
static void Bubble_Sort(int[] arr, int n)
{
boolean flag;
for(int i = 1; i < n; ++i)
{
flag = false;
for(int j = 0; j <= (n - i - 1); ++j)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = true;
}
}
if (flag == false)
break;
}
}
public static void main(String[] args)
{
int n = 5;
int[] arr = { 2, 0, 1, 4, 3 };
Bubble_Sort(arr, n);
System.out.print("The Sorted Array by " +
"using Bubble Sort is : ");
for(int i = 0; i < n; ++i)
System.out.print(arr[i] + " ");
}
}
|
Python3
def Bubble_Sort(arr, n):
flag = True
for i in range(1,n):
flag = False
for j in range(n-i):
if (arr[j] > arr[j + 1]):
arr[j], arr[j + 1] = arr[j + 1], arr[j]
flag = True
if (flag == False):
break
n = 5
arr = [2, 0, 1, 4, 3]
Bubble_Sort(arr, n)
print("The Sorted Array by using Bubble Sort is : ", end='')
for i in range(n):
print(arr[i], end= " ")
|
C#
using System;
public class GFG{
static void Bubble_Sort(int[] arr, int n)
{
bool flag;
for (int i = 1; i < n; ++i) {
flag = false;
for (int j = 0; j <= (n - i - 1); ++j) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = true;
}
}
if (flag == false)
break;
}
}
static public void Main ()
{
int n = 5;
int[] arr = { 2, 0, 1, 4, 3 };
Bubble_Sort(arr, n);
Console.Write("The Sorted Array by using Bubble Sort is : ");
for (int i = 0; i < n; ++i)
Console.Write(arr[i] + " ");
}
}
|
Javascript
<script>
function Bubble_Sort(arr, n)
{
Boolean(flag = true);
for(var i = 1; i < n; ++i)
{
flag = false;
for(var j = 0; j <= (n - i - 1); ++j)
{
if (arr[j] > arr[j + 1])
{
var temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
flag = true;
}
}
if (flag == false)
break;
}
}
var n = 5;
var arr = [ 2, 0, 1, 4, 3 ];
Bubble_Sort(arr, n);
document.write("The Sorted Array by " +
"using Bubble Sort is : ");
for(var i = 0; i < n; ++i)
document.write(arr[i] + " ");
</script>
|
OutputThe Sorted Array by using Bubble Sort is : 0 1 2 3 4
NOTE: This little tweak doesn’t change the worst case time complexity of the bubble sort algorithm but can improve its run time for particular cases.
Let us see the differences between Bubble Sort and Selection Sort in a tabular form -:
| | Selection Sort | Bubble Sort |
|---|
| 1. | Selection sorting is a sorting algorithm where we select the minimum element from the array and put that at its correct position. | Bubble sorting is a sorting algorithm where we check two elements and swap them at their correct positions. |
|---|
| 2. | Its Time complexity in the Best case is O(N^2) | Its Time complexity in the Best case is O(N) |
|---|
| 3. | Selection sort performs minimum number of swaps to sort the array | Bubble sort performs maximum number of swaps to sort the array |
|---|
| 4. | Its Time complexity in the worst case is O(N^2) | Its Time complexity in Worst case is O(N^2) |
|---|
| 5. | This sorting algorithm uses the selection method | This sorting algorithm uses exchanging method |
|---|
| 6. | It is an efficient sorting technique. | It is not an efficient sorting technique. |
|---|
| 7. | Is is not a stable algorithm | It is a stable algorithm |
|---|
| 8. | This method is faster. | This method is slower. |
|---|
References :
Lectures reading
Implement bubble sort c
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...