SciPy – Stats

The scipy.stats is the SciPy sub-package. It is mainly used for probabilistic distributions and statistical operations. There is a wide range of probability functions.

There are three classes:

Class	Description
rv_continuous	For continuous random variables, we can create specialized distribution subclasses and instances.
rv_discrete	For discrete random variables, we can create specialized distribution subclasses and instances.
rv_histogram	generate specific distribution histograms.

Continuous Random Variables

A continuous random variable is a probability distribution when the random variable X can have any value. The mean is defined by the location (loc) keyword. The standard deviation is determined by the scale (scale) keyword.

As we discussed that using the rv_continuous class we can create distributed subclasses and instances so there is a method called ‘norm’ which inherits from rv_continuous and this function will calculate the CDF for us.

Let X be a continuous random variable with PDF( (f) and CDF (F).

PDF – Probability Density Function

The PDF of a continuous random variable x satisfies the following conditions. If f\left ( x \right )\geq 0 for all x\in \mathbb{R} here f is piecewise continuous.

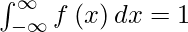
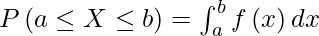
The CDF is found by integrating the PDF:

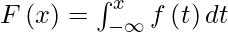
The pdf can be found by differentiating the CDF:

Python3

# Importing the numpy module for numpy array
import numpy as npy

# Importing the scipy.stats.norm
from scipy.stats import norm

# calculating the cdf for the numpy array
print(norm.cdf(npy.array([-2, 0, 2])))

Output:

[0.02275013 0.5        0.97724987]

Discrete Random Variables

Only a countable number of values can be assigned to discrete random variables. L is an additional integer parameter that can be added to any discrete distribution. The general distribution p and the standard distribution p₀ have the following relationship:

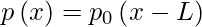
scipy.stats.circmean

Compute the circular mean for samples in a range. We will use the following function to calculate the circular mean:

Syntax:

scipy.stats.circmean(array, high=2*pi, low=0, axis=None, nan_policy=’propagate’)

where,

• Array – input array or samples.
• high (float or int ) – high boundary for sample. default high = 2 * pi.
• low ( float or int )  – low boundary for sample. default low = 0.
• axis ( int ) – Axis along which means are computed.
• nan_policy ( ‘propagate’, ‘raise’, ‘omit’ ) – Defines how to handle when input contains nan. ‘propagate’ returns nan, ‘raise’ throws an error, and ‘omit’ performs the calculations ignoring nan values. The default is ‘propagate’.

Python3

# importing the required package
from scipy.stats import circmean

# calculating the circular mean
print(circmean([0.4, 2.4, 3.6], high=4, low=2))
#                    |              |         |
#               -------------  ------------  ------------
#               sample array   higher bound  lower bound

Output:

2.254068341376122

scipy.stats.contingency.crosstab

Given the lists a and p, create a contingency table that counts the frequencies of the corresponding pairs.

Python3

# importing the required package
from scipy.stats.contingency import crosstab

# list p
a = ['A', 'B', 'A', 'A', 'B', 'B', 'A', 'A', 'B', 'B']

# list q
p = ['P', 'P', 'P', 'Q', 'R', 'R', 'Q', 'Q', 'R', 'R']

# result ndarray
print(crosstab(a, p))

# using the crosstab function and extracting
# the informations like - a's unique values,
# b's unique values and the final count of the pairs.
(auv, puv), cnt = crosstab(a,  p)

# printing list a's unique values
print(auv)

# printing list p's unique values
print(puv)

# printing the count object which tells us
# the pairs count for each unique values of a and p.
print(cnt)

Output:

((array(['A', 'B'], dtype='<U1'), array(['P', 'Q', 'R'], dtype='<U1')), array([[2, 3, 0],
       [1, 0, 4]]))
['A' 'B']
['P' 'Q' 'R']
[[2 3 0]
 [1 0 4]]

Note – In the above output, we have a ndarray, which consists of the different other arrays. The first value (array([‘A’, ‘B’]), dtype='<U1′) is basically the array of unique values in the list a, the second value (array([‘P’, ‘Q’, ‘R’]),dtype='<U1′) is basically the array of unique values in the list p, and the third value is the frequency of each pair of list a and list p.

list a = 

A

B

A

A

B

B

A

A

B

B

list b = 

P

P

P

Q

R

R

Q

Q

R

R

Result analysis

Above image observations – 

A - P = 2 
A - Q = 3 
A - R = 0

Above image observations:

B - P  = 1
B - Q  = 0
B - R  = 4

stats.describe()

This function basically calculates the several descriptive statistics of the argument array.

Syntax:

scipy.stats.describe(a, axis=0, ddof=1, bias=True, nan_policy=’propagate’)

where,

1. Input array – array for which we want to generate the statistics.
2. axis ( int , float ) { # optional } – Axis along which statistics are calculated. The default axis is 0.
3. ddof ( int ) { # optional } – Delta Degrees for variance. Default ddof = 1.
4. bias ( bool ) { # optional } – skewness and kurtosis calculations for statistical bias.
5. nan_policy – { ‘propagate’,’raise’,’omit’ } { # optional ) – Handle the NAN inputs.

Return:

1. nbos  ( int or ndarray ) – length of data along axis value.
2. minmax  ( tuple of ndarrays or floats ) – Minimum and Maximum value of input array along the given axis.
3. mean ( float or ndarray ) – mean of input array.
4. variance ( ndarray or float ) – variance of input array along the given axis.
5. skewness ( float or ndarray ) – skewness of input array along the given axis.
6. kurtosis ( ndarray or float ) – kurtosis of input array along the given axis.

Python3

# importing the stats and numpy module
from scipy import stats as st
import numpy as npy

# ID input array
array = npy.array([10, 20, 30, 40, 50, 60, 70, 80])

# calling the describe function
print(st.describe(array))

Output:

DescribeResult(
 nobs=8,
 minmax=(10, 80),
 mean=45.0,
 variance=600.0,
 skewness=0.0,
 kurtosis=-1.2380952380952381)

Python3

# importing the stats and numpy module
from scipy import stats as st
import numpy as npy

# 2D array
nd = npy.array([[5, 6], [2, 3], [5, 5],\
                [7, 9], [9, 8], [8, 7]])

# calling the describe function
print(st.describe(nd))

Output:

DescribeResult(nobs=6,
 minmax=(array([2, 3]),
 array([9, 9])),
 mean=array([6.        , 6.33333333]),
 variance=array([6.4       , 4.66666667]),
 skewness=array([-0.40594941, -0.3380617 ]),
 kurtosis=array([-0.9140625, -0.96     ]))

scipy.stats.kurtosis

Kurtosis quantifies how much of a probability distribution’s data are concentrated towards the mean as opposed to the tails. 

Kurtosis is the fourth central moment divided by the square of the variance. 

Syntax:

scipy.stats.kurtosis(a, axis=0, fisher=True, bias=True, nan_policy=’propagate’, *, keepdims=False

where,

1. Input array – Data for which the kurtosis is calculated..
2. axis ( int , float ) { # optional } – Axis along which statistics are calculated. The default axis is 0.
3. fisher ( bool ) { # optional } – If True, Fisher’s definition is used. If False, Pearson’s definition is used.
4. bias ( bool ) { # optional } – If False, then the calculations are corrected for statistical bias.
5. nan_policy – { ‘propagate’,’raise’,’omit’ } { # optional ) – Handle the NAN inputs.
6. keepdims( bool ) ( # optional ) – default is false.  broadcast result correctly against the input array.

Returns:

• kurtosis array – along the given axis.

Python3

# importing the stats module
from scipy import stats as st

# the random dataset
dataset = st.norm.rvs(size=88)

# calling the kurtosis function
print(st.kurtosis(dataset))

Output:

0.04606780907050423

scipy.stats.mstats.zscore

The Z-score provides information on how far a given value deviates from the standard deviation. When a data point’s Z-score is 0, it means that it has the same score as the mean. 

Z = ( Observed Value ( x ) – mean ( μ ) ) / standard deviation ( σ )

Calculate the z score for each value in the input array in comparison to the sample mean and standard deviation.

Function parameters –

Syntax:

scipy.stats.mstats.zscore(a, axis=0, ddof=0, nan_policy=’propagate’)

where,

1. Input array – sample input array.
2. axis ( int , float ) { # optional } – Axis along which statistics are calculated. The default axis is 0.
3. ddof ( int ) { # optional } – Degrees of freedom correction in the calculation of the standard deviation. The default value of ddof is 0.
4. nan_policy – { ‘propagate’,’raise’,’omit’ } { # optional ) – Handle the NAN inputs.

Returns:

• zscore – array – The z-scores of input array a, normalised by mean and standard deviation.

Python3

# importing the stats module
from scipy import stats as st

# the random 1D ARRAY ( dataset )
dataset = [0.02, 0.5, 0.01, 0.33, 0.51, 1.0, 0.03]

# the random 2D ARRAY ( dataset )
nd = [[5.1, 6.1], [2.1, 3.1], [5.1, 5.1],\
      [7.1, 9.1], [9.1, 8.1], [8.1, 7.1]]

# calling the kurtosis function
# 1D dataset
print(st.zscore(dataset))

# calling the kurtosis function
# 2D dataset
print(st.zscore(nd))

Output:

[-0.95649434  0.46555034 -0.98612027 -0.03809048  0.49517627  1.94684689
 -0.92686841]
[[-0.4330127  -0.16903085]
 [-1.73205081 -1.69030851]
 [-0.4330127  -0.6761234 ]
 [ 0.4330127   1.35224681]
 [ 1.29903811  0.84515425]
 [ 0.8660254   0.3380617 ]]

scipy.stats.skew

We can determine the direction of outliers from skewness. The tail of a distribution curve has a longer right side when there is a positive skew. Accordingly, the distribution curve’s outliers are farther from the mean on the left and closer to it on the right. Skewness just conveys the direction of outliers; it doesn’t provide information on the number of outliers. 

Compute the sample skewness of a data set. Skewness should be close to zero for normally distributed data. A skewness value greater than zero indicates that the right tail of a unimodal continuous distribution has more weight. 

Syntax:

scipy.stats.skew(a, axis=0, bias=True, nan_policy=’propagate’, *, keepdims=False)

where,

1. Input array
2. axis ( int , float ) { # optional } – Axis along which statistics are calculated. The default axis is 0.
3. bias ( bool ) { # optional } – If False, then the calculations are corrected for statistical bias.
4. nan_policy – { ‘propagate’,’raise’,’omit’ } { # optional ) – Handle the NAN inputs.
5. keepdims( bool ) ( # optional ) – default is false.  broadcast result correctly against the input array.

Return:

• skewness – ndarray

Python3

# importing the stats module
from scipy import stats as st

# ID input array
array = [99, 10, 30, 55, 50, 0, 90, 0]

# calling the skew function
print(st.skew(array))

Output:

0.3260023450293658

scipy.stats.energy_distance

Distance between two probability distributions. Suppose two distributions u and v and their CDF are U and V, two random variables X and Y are there, then the energy distance will be the square root of:

 D²(U,V) = 2E || X – Y || – E || X – X’ || – E || Y – Y’ || > 0,

•  || denotes the length of a vector

Compute the energy distance between two 1D distributions.

Python3

# importing the stats module
from scipy import stats as st

# calling the function
print(st.energy_distance([5, 10], [10, 20],\
                         [20, 30], [30, 40]))

Output:

2.851422845685634

scipy.stats.mode

Return an array of the most common values in the input array.

Python3

# importing the stats module
from scipy import stats as st

# sample input array
array = [[2, 3], [3, 1], [1, 3],\
         [3, 3], [4, 2], [4, 4],\
         [1, 2], [5, 6]]

# calling the mode function
print(st.mode(array))

Output:

ModeResult(mode=array([[1, 3]]), count=array([[2, 3]]))

scipy.stats.variation

The coefficient of variation – Standard deviation divided by the mean.

Python3

# importing the stats module
from scipy import stats as st

# sample input array
array = [[2, 3], [3, 1], [1, 3],\
         [3, 3], [4, 2], [4, 4],\
         [1, 2], [5, 6]]

# calling the function
print(st.variation(array, ddof=1))

Output:

[0.5070393  0.50395263]

scipy.stats.rankdata

Assign ranks to data, dealing with ties appropriately.

Python3

# importing the stats module
from scipy import stats as st

# sample input array
array = [2, 3, 15, 1, 6, 9, 8, 4, 5, 10]

# calling the function
print(st.rankdata(array))

Output:

[ 2.  3. 10.  1.  6.  8.  7.  4.  5.  9.]