scipy stats.kurtosis() function | Python
Last Updated :
20 Jun, 2022
scipy.stats.kurtosis(array, axis=0, fisher=True, bias=True) function calculates the kurtosis (Fisher or Pearson) of a data set. It is the fourth central moment divided by the square of the variance. It is a measure of the “tailedness” i.e. descriptor of shape of probability distribution of a real-valued random variable. In simple terms, one can say it is a measure of how heavy tail is compared to a normal distribution. Its formula – 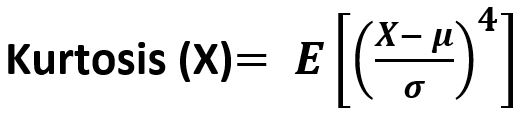
Parameters : array : Input array or object having the elements. axis : Axis along which the kurtosis value is to be measured. By default axis = 0. fisher : Bool; Fisher’s definition is used (normal 0.0) if True; else Pearson’s definition is used (normal 3.0) if set to False. bias : Bool; calculations are corrected for statistical bias, if set to False. Returns : Kurtosis value of the normal distribution for the data set.
Code #1:
Python3
from scipy.stats import kurtosis
import numpy as np
import pylab as p
x1 = np.linspace( -5, 5, 1000 )
y1 = 1./(np.sqrt(2.*np.pi)) * np.exp( -.5*(x1)**2 )
p.plot(x1, y1, '*')
print( '\nKurtosis for normal distribution :', kurtosis(y1))
print( '\nKurtosis for normal distribution :',
kurtosis(y1, fisher = False))
print( '\nKurtosis for normal distribution :',
kurtosis(y1, fisher = True))
|
Output :
Kurtosis for normal distribution : -0.3073930877422071
Kurtosis for normal distribution : 2.692606912257793
Kurtosis for normal distribution : -0.3073930877422071
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...