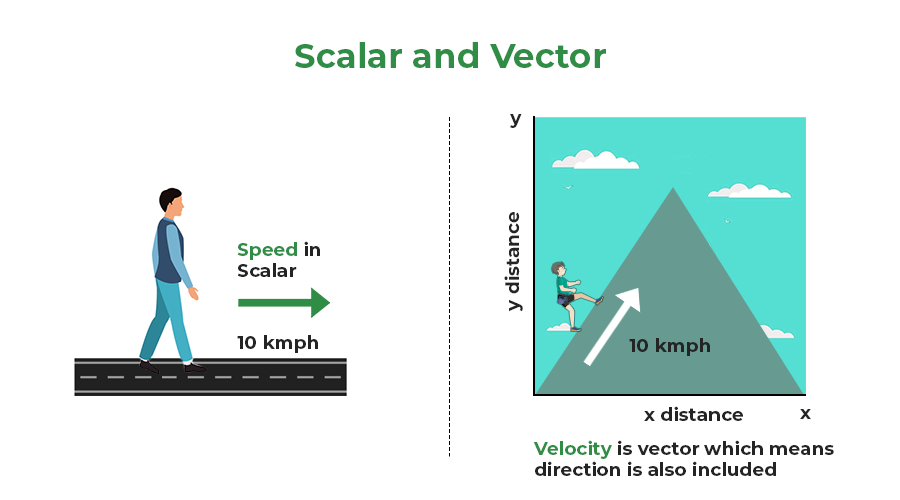
Scalar and Vector

Scalar and Vector Quantities are used to describe the motion of an object. Scalar Quantities are defined as physical quantities that have magnitude or size only. For example, distance, speed, mass, density, etc. However, vector quantities are those physical quantities that have both magnitude and direction like displacement, velocity, acceleration, force, etc. It should be noted that when a vector quantity changes its magnitude and direction also change similarly, when a scalar quantity changes, only its magnitude changes.

Scalar Quantities Definition

A scalar quantity is a physical quantity that has only magnitude and no direction. In other words, a scalar quantity is described only by a number and a unit, and it does not have any associated direction or vector.

Examples of scalar quantities include temperature, mass, time, distance, speed, and energy. These quantities can be measured using instruments such as thermometers, scales, stopwatches, rulers, speedometers, and wattmeters.

Scalar quantities can be added, subtracted, multiplied, and divided using standard mathematical operations. For example, if a car travels 100 kilometers in 2 hours, its average speed can be calculated as 50 kilometers per hour (km/h) by dividing the distance traveled by the time taken.

Scalar quantities are often contrasted with vector quantities, which have both magnitude and direction, such as velocity, acceleration, force, and displacement. Vector quantities are typically represented graphically using arrows to show their direction and magnitude, while scalar quantities are represented using only a number and a unit.

There exist many forms of scalar quantities some of them are listed below:

• Mass
• Speed
• Distance
• Time
• Area
• Volume
• Density
• Energy
• Temperature
• Electric Charge
• Gravitational force

Vector Quantities 

A vector quantity is a physical quantity that has both magnitude and direction. In other words, a vector quantity is described by a number, a unit, and a direction.

Examples of vector quantities include velocity, acceleration, force, displacement, and momentum. These quantities are commonly represented graphically using arrows to show both their direction and magnitude.

For example, if a car is traveling at a velocity of 50 km/h towards the east, its velocity can be represented as a vector with an arrow pointing to the right (east) and a length of 50 km/h.

Vector quantities can be added, subtracted, multiplied, and divided using vector algebra. For example, if a force of 10 N is applied to an object in the north direction, and a force of 5 N is applied in the east direction, the resultant force can be calculated using vector addition as a force of √125 N towards the northeast direction.

Vector quantities are used in many fields of science and engineering, such as mechanics, electromagnetism, fluid dynamics, and quantum mechanics. They are essential for describing the behavior of physical systems and making predictions about their future states.

There are countless examples of vector quantities in daily life. The list of some of them is down below!

• Velocity
• Force
• Pressure
• Displacement
• Acceleration
• Thrust
• Linear momentum
• Electric field
• Polarization
• Weight

Vector Notation

Vector notation is a way or notation used to represent a quantity that is a vector, through an arrow (⇢) above its symbol, as shown below:

Scalar and Vector Quantity

The differences between Scalar and Vector Quantities are shown in the table added below,

Difference Between Scalar and Vector Quantity
Scalar	Vector
Scalar quantities have magnitude or size only.	Vector quantities have both magnitude and direction.
It is known that every scalar exists in one dimension only.	Vector quantities can exist in one, two, or three-dimension.
Whenever there is a change in a scalar quantity, can correspond to a change in its magnitude also.	Any change in a vector quantity can correspond to cha change in either its magnitude or direction or both.
These quantities can not be resolved into their components.	These quantities can be resolved into their components, using the sine or cosine of the adjacent angle.
Any mathematical process that involves more than two scalar quantities will only give scalars.	Mathematical operations on two or more vectors can provide either a scalar or a vector as a result. For instance, the dot product of two vectors only produces a scalar, whereas the cross product, sum, or subtraction of two vectors gives a vector.
Some examples of Scalar quantities are: Mass Speed Distance Time Area Volume	Some examples of Vector quantities are: Velocity Force Pressure Displacement Acceleration

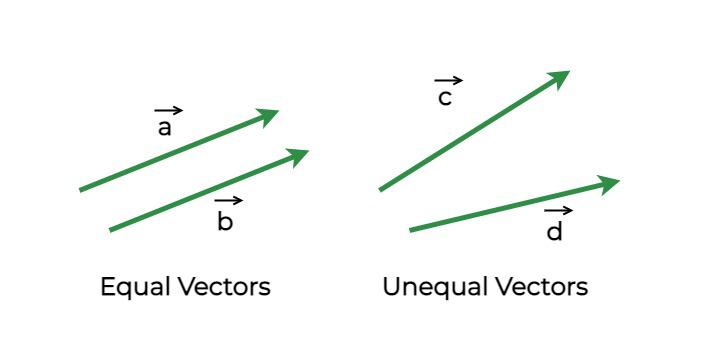
Equality of Vectors

Two vectors are considered to be equal when they have the same magnitude and same direction. The figure below shows two vectors that are equal, notice that these vectors are parallel to each other and have the same length. The second part of the figure shows two unequal vectors, which even though have the same magnitude, are not equal because they have different directions. 

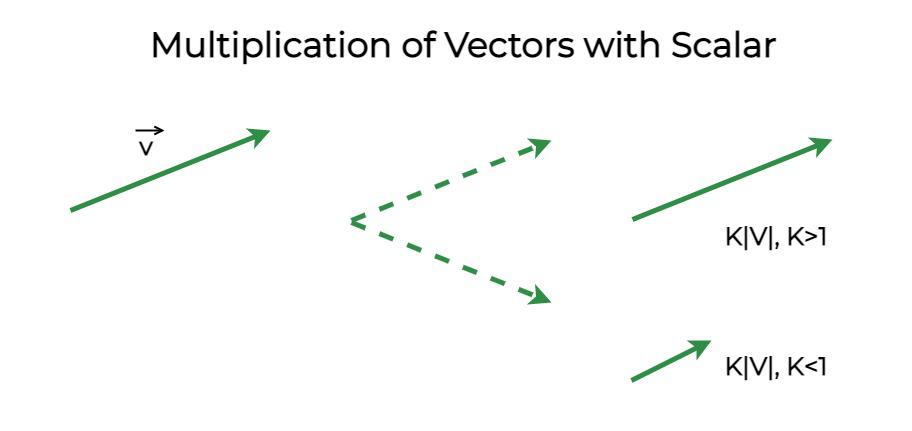
Multiplication of Vectors with Scalar

Multiplying a vector a with a constant scalar k gives a vector whose direction is the same but the magnitude is changed by a factor of k. The figure shows the vector after and before it is multiplied by the constant k. In mathematical terms, this can be rewritten as, 

[Tex]|k\vec{v}| = k|\vec{v}|[/Tex]

if k > 1, the magnitude of the vector increase while it decreases when the k < 1. 

Addition of Vectors

Vectors cannot be added by usual algebraic rules. While adding two vectors, the magnitude and the direction of the vectors must be taken into account. Triangle law is used to add two vectors, the diagram below shows two vectors “a” and “b” and the resultant is calculated after their addition. Vector addition follows commutative property, this means that the resultant vector is independent of the order in which the two vectors are added. 

[Tex]\vec{a} + \vec{b} = \vec{c} [/Tex]

[Tex]\vec{a} + \vec{b} = \vec{b} + \vec{a}     [/Tex]  – (Commutative Property)

Triangle Law of Vector Addition

Consider the vectors given in the figure above. The line PQ represents the vector “p”, and QR represents the vector “q”. The line QR represents the resultant vector. The direction of AC is from A to C.  

Line AC represents, 

[Tex]\vec{p} + \vec{q} [/Tex]

The magnitude of the resultant vector is given by, 

[Tex]\sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)} [/Tex]

θ represents the angle between the two vectors. Let φ be the angle made by the resultant vector with the vector p.

[Tex]tan (\phi) = \dfrac{q\sin\theta}{p + q\cos\theta} [/Tex]

The above formula is known as the Triangle Law of Vector Addition.

Parallelogram Law of Vector Addition

This law is just another way of understanding vector addition. This law states that if two vectors acting on the same point are represented by the sides of the parallelogram, then the resultant vector of these vectors is represented by the diagonals of the parallelograms. The figure below shows these two vectors represented on the side of the parallelogram. 

Examples on Scalar and Vector

Example 1: Find the magnitude of v = i + 4j. 

Solution:

|v| = [Tex]\sqrt{a^2 + b^2} [/Tex]

a = 1, b = 4

|v| = [Tex]\sqrt{1^2 + 4^2} [/Tex]

|v| = [Tex]\sqrt{1^2 + 4^2} [/Tex]

|v| = √17

Example 2: A vector is given by, v = i + 4j. Find the magnitude of the vector when it is scaled by a constant of 5. 

Solution:

|v| = [Tex]\sqrt{a^2 + b^2} [/Tex]

5|v| = |5v| 

a = 1, b = 4

|5v|

|5(i + 4j)| 

|5i + 20j| 

|v| = [Tex]\sqrt{5^2 + 20^2} [/Tex]

|v| = [Tex]\sqrt{25 + 400} [/Tex]

|v| = √425

Example 3: A vector is given by, v = i + j. Find the magnitude of the vector when it is scaled by a constant of 0.5. 

Solution:

|v| = [Tex]\sqrt{a^2 + b^2} [/Tex]

0.5|v| = |0.5v| 

a = 1, b = 1

|0.5v|

|0.5(i + j)| 

|0.5i + 0.5j| 

|v| = [Tex]\sqrt{0.5^2 + 0.5^2} [/Tex]

|v| = [Tex]\sqrt{0.25 + 0.25} [/Tex]

|v| = √0.5

Example 4: Two vectors with magnitude 3 and 4. These vectors have a 90° angle between them. Find the magnitude of the resultant vectors. 

Solution:

Let the two vectors be given by p and q. Then resultant vector “r” is given by, 

[Tex]|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)} [/Tex]

|p| = 3, |q| = 4 and [Tex]\theta = 90^o [/Tex]

[Tex]|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)} [/Tex]

[Tex]|r| = \sqrt{|3|^2 + |4|^2 + 2|3||4|cos(90)} [/Tex]

[Tex]|r| = \sqrt{|3|^2 + |4|^2} [/Tex]

[Tex]|r| = \sqrt{9 + 16} [/Tex]

[Tex]|r| = \sqrt{9 + 16}                    [/Tex]

|r| = 5

Example 5: Two vectors with magnitude 10 and 9. These vectors have a 60° angle between them. Find the magnitude of the resultant vectors. 

Solution:

Let the two vectors be given by p and q. Then resultant vector “r” is given by, 

[Tex]|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)} [/Tex]

|p| = 10, |q| = 9 and [Tex]\theta = 60^o [/Tex]

[Tex]|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)} [/Tex]

[Tex]|r| = \sqrt{|10|^2 + |9|^2 + 2|10||9|cos(60)} [/Tex]

[Tex]|r| = \sqrt{|10|^2 + |9|^2 + (10)(9)} [/Tex]

[Tex]|r| = \sqrt{100 + 81 + 90} [/Tex]

[Tex]|r| = \sqrt{271}   [/Tex]

Scalars and Vectors-FAQs

1. What do you mean by Scalars and Vectors, in physics?

Scalars are the physical quantities that have magnitude or size only. While vectors are the physical quantities that have both magnitude and direction.

2. What are examples of Vectors Quantities?

Here are some important examples of vectors quantites are:

• Velocity
• Force
• Pressure
• Displacement
• Acceleration
• Thrust

3. What are some Scalar Quantities?

Here are some important examples of scalars are:

• Mass
• Speed
• Distance
• Time
• Area
• Volume

4. Is Force is a Scalar or a Vector Quantity?

Since force is a physical quantity that has both magnitude and direction. Therefore, it’s a vector quantity.

5. What is Difference Between Distance and Displacement?

The main difference between distance and displacement is that the distance has magnitude only and is a scalar quantity. However, displacement has both magnitude and direction so it is a vector quantity.