Runs Test of Randomness in Python
Last Updated :
08 Jun, 2020
Random numbers are an imperative part of many systems, including simulations, cryptography and much more. So the ability to produce values randomly, with no apparent logic and predictability, becomes a prime function. Since computers cannot produce values which are completely random, algorithms, known as pseudorandom number generators (PRNG) are used to accomplish this task.
The values produced by PRNGs are not truly random and depend on the initial value provided to the algorithm, known as the seed value. The property of a pseudorandom sequence being reproducible, given it’s seed value is essential for its application in simulations, such as the Monte Carlo Simulation, where the system might need to be tested on the same sequence more than once.
Some of the most popular and highly used PRNGs are:
- Mersenne Twister: Used as the default random number generator in Python, R, Excel, Matlab, Ruby and many more popular software systems.
- Linear Congruential Generator: Used in C++ and Java
- Wichmann-Hill Generator: Used in Excel and was the default in Python 2.2
- Park-Miller Generator
- Middle Square Weyl Sequence
To ensure that the values generated by the PRNG are as close to random as possible, several statistical tests including the Diehard tests, TestU01 series, Chi-Square test and the Runs test of Randomness are used. This article focuses on the Runs Test of Randomness.
What is the Runs Test?
Runs test of randomness is a statistical test that is used to check the randomness in data. It is a nonparametric test and uses runs of data to decide whether the presented data is random or tends to follow a pattern. A run is defined as a series of increasing values or decreasing values. The number of increasing, or decreasing, values is the length of the run.
The first step in the runs test is to count the number of runs in the data sequence. There are several ways to define runs, however, in all cases the formulation must produce a dichotomous sequence of values. In our case, the values above the median are treated as positive and values below the median as negative. A run is defined as a series of consecutive positive or negative values.
Applying Runs Test
- The first step in applying this test is to formulate the null and alternate hypothesis.
Hnull : The sequence was produced in a random manner
Halt : The sequence was not produced in a random manner
- Calculate the test statistic, Z as :
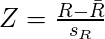 Where,
R = The number of observed runs
R' = The number of expected runs, given as
Where,
R = The number of observed runs
R' = The number of expected runs, given as
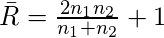 SR = Standard Deviation of the number of runs
SR = Standard Deviation of the number of runs
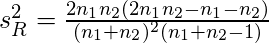 With n1 and n2 = the number of positive and
negative values in the series
With n1 and n2 = the number of positive and
negative values in the series
- Compare the value of the calculated Z-statistic with Zcritical for a given level of confidence (Zcritical =1.96 for confidence level of 95%) . The null hypothesis is rejected i.e. the numbers are declared not to be random, if |Z|>Zcritical .
Example:
Python3
import random
import math
import statistics
def runsTest(l, l_median):
runs, n1, n2 = 0, 0, 0
for i in range(len(l)):
if (l[i] >= l_median and l[i-1] < l_median) or \
(l[i] < l_median and l[i-1] >= l_median):
runs += 1
if(l[i]) >= l_median:
n1 += 1
else:
n2 += 1
runs_exp = ((2*n1*n2)/(n1+n2))+1
stan_dev = math.sqrt((2*n1*n2*(2*n1*n2-n1-n2))/ \
(((n1+n2)**2)*(n1+n2-1)))
z = (runs-runs_exp)/stan_dev
return z
l = []
for i in range(100):
l.append(random.random())
l_median= statistics.median(l)
Z = abs(runsTest(l, l_median))
print('Z-statistic= ', Z)
|
Output:
Z-statistic= 1.809160364503323
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...