Runge-Kutta 4th Order Method to Solve Differential Equation

Given the following inputs, 

• An ordinary differential equation that defines value of dy/dx in the form x and y.
• Initial value of y, i.e., y(0)

Thus we are given below.

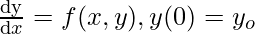
The task is to find the value of the unknown function y at a given point x.
The Runge-Kutta method finds the approximate value of y for a given x. Only first-order ordinary differential equations can be solved by using the Runge Kutta 4th order method.
Below is the formula used to compute next value y_n+1 from previous value y_n. The value of n are 0, 1, 2, 3, ….(x – x0)/h. Here h is step height and x_n+1 = x₀ + h
. Lower step size means more accuracy.

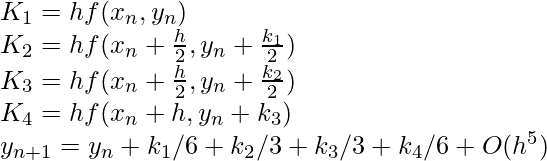
The formula basically computes next value y_n+1 using current y_n plus weighted average of four increments. 

• k₁ is the increment based on the slope at the beginning of the interval, using y
• k₂ is the increment based on the slope at the midpoint of the interval, using y + hk₁/2.
• k₃ is again the increment based on the slope at the midpoint, using  y + hk₂/2.
• k₄ is the increment based on the slope at the end of the interval, using y + hk₃.

The method is a fourth-order method, meaning that the local truncation error is on the order of O(h⁵), while the total accumulated error is order O(h⁴).
Source: https://en.wikipedia.org/wiki/Runge%E2%80%93Kutta_methods

Below is the implementation for the above formula. 

C++

// C++ program of the above approach
#include <bits/stdc++.h>
using namespace std;

// A sample differential equation "dy/dx = (x - y)/2"
float dydx(float x, float y)
{
    return((x - y)/2);
}

// Finds value of y for a given x using step size h
// and initial value y0 at x0.
float rungeKutta(float x0, float y0, float x, float h)
{
    // Count number of iterations using step size or
    // step height h
    int n = (int)((x - x0) / h);

    float k1, k2, k3, k4, k5;

    // Iterate for number of iterations
    float y = y0;
    for (int i=1; i<=n; i++)
    {
        // Apply Runge Kutta Formulas to find
        // next value of y
        k1 = h*dydx(x0, y);
        k2 = h*dydx(x0 + 0.5*h, y + 0.5*k1);
        k3 = h*dydx(x0 + 0.5*h, y + 0.5*k2);
        k4 = h*dydx(x0 + h, y + k3);

        // Update next value of y
        y = y + (1.0/6.0)*(k1 + 2*k2 + 2*k3 + k4);;

        // Update next value of x
        x0 = x0 + h;
    }

    return y;
}

// Driver Code
int main()
{
    float x0 = 0, y = 1, x = 2, h = 0.2;
    cout << "The value of y at x is : " <<
            rungeKutta(x0, y, x, h);

    return 0;
}

// This code is contributed by code_hunt.

C

// C program to implement Runge Kutta method
#include<stdio.h>

// A sample differential equation "dy/dx = (x - y)/2"
float dydx(float x, float y)
{
    return((x - y)/2);
}

// Finds value of y for a given x using step size h
// and initial value y0 at x0.
float rungeKutta(float x0, float y0, float x, float h)
{
    // Count number of iterations using step size or
    // step height h
    int n = (int)((x - x0) / h);

    float k1, k2, k3, k4, k5;

    // Iterate for number of iterations
    float y = y0;
    for (int i=1; i<=n; i++)
    {
        // Apply Runge Kutta Formulas to find
        // next value of y
        k1 = h*dydx(x0, y);
        k2 = h*dydx(x0 + 0.5*h, y + 0.5*k1);
        k3 = h*dydx(x0 + 0.5*h, y + 0.5*k2);
        k4 = h*dydx(x0 + h, y + k3);

        // Update next value of y
        y = y + (1.0/6.0)*(k1 + 2*k2 + 2*k3 + k4);;

        // Update next value of x
        x0 = x0 + h;
    }

    return y;
}

// Driver method
int main()
{
    float x0 = 0, y = 1, x = 2, h = 0.2;
    printf("\nThe value of y at x is : %f",
            rungeKutta(x0, y, x, h));
    return 0;
}

Java

// Java program to implement Runge Kutta method
import java.io.*;
class differential
{
    double dydx(double x, double y)
    {
        return ((x - y) / 2);
    }

    // Finds value of y for a given x using step size h
    // and initial value y0 at x0.
    double rungeKutta(double x0, double y0, double x, double h)
    {
        differential d1 = new differential();
        // Count number of iterations using step size or
        // step height h
        int n = (int)((x - x0) / h);

        double k1, k2, k3, k4, k5;

        // Iterate for number of iterations
        double y = y0;
        for (int i = 1; i <= n; i++)
        {
            // Apply Runge Kutta Formulas to find
            // next value of y
            k1 = h * (d1.dydx(x0, y));
            k2 = h * (d1.dydx(x0 + 0.5 * h, y + 0.5 * k1));
            k3 = h * (d1.dydx(x0 + 0.5 * h, y + 0.5 * k2));
            k4 = h * (d1.dydx(x0 + h, y + k3));

            // Update next value of y
            y = y + (1.0 / 6.0) * (k1 + 2 * k2 + 2 * k3 + k4);

            // Update next value of x
            x0 = x0 + h;
        }
        return y;
    }

    public static void main(String args[])
    {
        differential d2 = new differential();
        double x0 = 0, y = 1, x = 2, h = 0.2;

        System.out.println("\nThe value of y at x is : "
                    + d2.rungeKutta(x0, y, x, h));
    }
}

// This code is contributed by Prateek Bhindwar

Python3

# Python program to implement Runge Kutta method
# A sample differential equation "dy / dx = (x - y)/2"
def dydx(x, y):
    return ((x - y)/2)

# Finds value of y for a given x using step size h
# and initial value y0 at x0.
def rungeKutta(x0, y0, x, h):
    # Count number of iterations using step size or
    # step height h
    n = (int)((x - x0)/h)
    # Iterate for number of iterations
    y = y0
    for i in range(1, n + 1):
        "Apply Runge Kutta Formulas to find next value of y"
        k1 = h * dydx(x0, y)
        k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
        k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2)
        k4 = h * dydx(x0 + h, y + k3)

        # Update next value of y
        y = y + (1.0 / 6.0)*(k1 + 2 * k2 + 2 * k3 + k4)

        # Update next value of x
        x0 = x0 + h
    return y

# Driver method
x0 = 0
y = 1
x = 2
h = 0.2
print ('The value of y at x is:', rungeKutta(x0, y, x, h))

# This code is contributed by Prateek Bhindwar

C#

// C# program to implement Runge
// Kutta method
using System;

class GFG {

    static double dydx(double x, double y)
    {
        return ((x - y) / 2);
    }

    // Finds value of y for a given x
    // using step size h and initial
    // value y0 at x0.
    static double rungeKutta(double x0,
                double y0, double x, double h)
    {

        // Count number of iterations using
        // step size or step height h
        int n = (int)((x - x0) / h);

        double k1, k2, k3, k4;

        // Iterate for number of iterations
        double y = y0;

        for (int i = 1; i <= n; i++)
        {

            // Apply Runge Kutta Formulas
            // to find next value of y
            k1 = h * (dydx(x0, y));

            k2 = h * (dydx(x0 + 0.5 * h,
                             y + 0.5 * k1));

            k3 = h * (dydx(x0 + 0.5 * h,
                            y + 0.5 * k2));

            k4 = h * (dydx(x0 + h, y + k3));

            // Update next value of y
            y = y + (1.0 / 6.0) * (k1 + 2
                       * k2 + 2 * k3 + k4);

            // Update next value of x
            x0 = x0 + h;
        }

        return y;
    }

    // Driver code
    public static void Main()
    {

        double x0 = 0, y = 1, x = 2, h = 0.2;

        Console.WriteLine("\nThe value of y"
                             + " at x is : "
                 + rungeKutta(x0, y, x, h));
    }
}

// This code is contributed by Sam007.

PHP

<?php
// PHP program to implement
// Runge Kutta method

// A sample differential equation
// "dy/dx = (x - y)/2"
function dydx($x, $y)
{
    return(($x - $y) / 2);
}

// Finds value of y for a
// given x using step size h
// and initial value y0 at x0.
function rungeKutta($x0, $y0, $x, $h)
{

    // Count number of iterations
    // using step size or step
    // height h
    $n = (($x - $x0) / $h);

    $k1; $k2; $k3; $k4; $k5;

    // Iterate for number
    // of iterations
    $y = $y0;
    for($i = 1; $i <= $n; $i++)
    {

        // Apply Runge Kutta
        // Formulas to find
        // next value of y
        $k1 = $h * dydx($x0, $y);
        $k2 = $h * dydx($x0 + 0.5 * $h,
                        $y + 0.5 * $k1);
        $k3 = $h * dydx($x0 + 0.5 * $h,
                        $y + 0.5 * $k2);
        $k4 = $h * dydx($x0 + $h, $y + $k3);

        // Update next value of y
        $y = $y + (1.0 / 6.0) * ($k1 + 2 *
                    $k2 + 2 * $k3 + $k4);;

        // Update next value of x
        $x0 = $x0 + $h;
    }

    return $y;
}

    // Driver method
    $x0 = 0;
    $y = 1;
    $x = 2;
    $h = 0.2;
    echo "The value of y at x is : ",
          rungeKutta($x0, $y, $x, $h);

// This code is contributed by anuj_67.
?>

Javascript

<script>

// Javascript program to implement Runge Kutta method

// A sample differential equation "dy/dx = (x - y)/2"
function dydx(x, y)
{
    return((x - y) / 2);
}

// Finds value of y for a given x using step size h
// and initial value y0 at x0.
function rungeKutta(x0, y0, x, h)
{

    // Count number of iterations using
    // step size or step height h
    let n = parseInt((x - x0) / h, 10);

    let k1, k2, k3, k4, k5;

    // Iterate for number of iterations
    let y = y0;
    for(let i = 1; i <= n; i++)
    {

        // Apply Runge Kutta Formulas to find
        // next value of y
        k1 = h * dydx(x0, y);
        k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1);
        k3 = h * dydx(x0 + 0.5 * h, y + 0.5 * k2);
        k4 = h * dydx(x0 + h, y + k3);

        // Update next value of y
        y = y + (1 / 6) * (k1 + 2 * k2 +
                            2 * k3 + k4);;

        // Update next value of x
        x0 = x0 + h;
    }
    return y.toFixed(6);
}

// Driver code
let x0 = 0, y = 1, x = 2, h = 0.2;

document.write("The value of y at x is : " +
               rungeKutta(x0, y, x, h));

// This code is contributed by divyesh072019

</script>

Output

The value of y at x is : 1.10364

Time Complexity: O(n), where n is (x-x0)/h.
Auxiliary Space: O(1) as constant space for variables is being used

Some useful resources for detailed examples and more explanation. 
http://w3.gazi.edu.tr/~balbasi/mws_gen_ode_txt_runge4th.pdf
https://www.youtube.com/watch?v=kUcc8vAgoQ0

This article is contributed by Arpit Agarwal. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above