Runge-Kutta 2nd order method to solve Differential equations //
Last Updated :
10 Apr, 2023
Given the following inputs:
- An ordinary differential equation that defines the value of dy/dx in the form x and y.
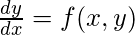
- Initial value of y, i.e., y(0).
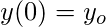
The task is to find the value of unknown function y at a given point x, i.e. y(x).
Example:
Input: x0 = 0, y0 = 1, x = 2, h = 0.2
Output: y(x) = 0.645590
Input: x0 = 2, y0 = 1, x = 4, h = 0.4;
Output: y(x) = 4.122991
Approach:
The Runge-Kutta method finds an approximate value of y for a given x. Only first-order ordinary differential equations can be solved by using the Runge-Kutta 2nd-order method.
Below is the formula used to compute the next value yn+1 from the previous value yn. Therefore:
yn+1 = value of y at (x = n + 1)
yn = value of y at (x = n)
where
0 ? n ? (x - x0)/h
h is step height
xn+1 = x0 + h
The essential formula to compute the value of y(n+1):
K1 = h * f(x,y)
K2 = h * f(x/2, y/2) or K1/2
yn+1 = yn + K2 + (h3)
The formula basically computes the next value yn+1 using current yn plus the weighted average of two increments:
- K1 is the increment based on the slope at the beginning of the interval, using y.
- K2 is the increment based on the slope at the midpoint of the interval, using (y + h*K1/2).
The method is a second-order method, meaning that the local truncation error is in the order of O(h3), while the total accumulated error is order of O(h4).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
float dydx(float x, float y) { return (x + y - 2); }
float rungeKutta(float x0, float y0, float x, float h)
{
int n = (int)((x - x0) / h);
float k1, k2;
float y = y0;
for (int i = 1; i <= n; i++) {
k1 = h * dydx(x0, y);
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1);
y = y + (1.0 / 6.0) * (k1 + 2 * k2);
x0 = x0 + h;
}
return y;
}
int main()
{
float x0 = 0, y = 1, x = 2, h = 0.2;
cout << fixed << setprecision(6)
<< "y(x) = " << rungeKutta(x0, y, x, h);
return 0;
}
|
Java
class GFG {
static double dydx(double x, double y)
{
return (x + y - 2);
}
static double rungeKutta(double x0, double y0, double x,
double h)
{
int n = (int)((x - x0) / h);
double k1, k2;
double y = y0;
for (int i = 1; i <= n; i++) {
k1 = h * dydx(x0, y);
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1);
y = y + (1.0 / 6.0) * (k1 + 2 * k2);
x0 = x0 + h;
}
return y;
}
public static void main(String[] args)
{
double x0 = 0, y = 1, x = 2, h = 0.2;
System.out.println(rungeKutta(x0, y, x, h));
}
}
|
Python3
def dydx(x, y):
return (x + y - 2)
def rungeKutta(x0, y0, x, h):
n = round((x - x0) / h)
y = y0
for i in range(1, n + 1):
k1 = h * dydx(x0, y)
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1)
y = y + (1.0 / 6.0) * (k1 + 2 * k2)
x0 = x0 + h
return y
if __name__ == "__main__":
x0 = 0
y = 1
x = 2
h = 0.2
print("y(x) =", rungeKutta(x0, y, x, h))
|
C
#include <stdio.h>
float dydx(float x, float y) { return (x + y - 2); }
float rungeKutta(float x0, float y0, float x, float h)
{
int n = (int)((x - x0) / h);
float k1, k2;
float y = y0;
for (int i = 1; i <= n; i++) {
k1 = h * dydx(x0, y);
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1);
y = y + (1.0 / 6.0) * (k1 + 2 * k2);
x0 = x0 + h;
}
return y;
}
int main()
{
float x0 = 0, y = 1, x = 2, h = 0.2;
printf("y(x) = %f", rungeKutta(x0, y, x, h));
return 0;
}
|
C#
using System;
class GFG {
static double dydx(double x, double y)
{
return (x + y - 2);
}
static double rungeKutta(double x0, double y0, double x,
double h)
{
int n = (int)((x - x0) / h);
double k1, k2;
double y = y0;
for (int i = 1; i <= n; i++) {
k1 = h * dydx(x0, y);
k2 = h * dydx(x0 + 0.5 * h, y + 0.5 * k1);
y = y + (1.0 / 6.0) * (k1 + 2 * k2);
x0 = x0 + h;
}
return y;
}
public static void Main(string[] args)
{
double x0 = 0, y = 1, x = 2, h = 0.2;
Console.WriteLine(rungeKutta(x0, y, x, h));
}
}
|
Javascript
<script>
function dydx(x, y)
{
return (x + y - 2);
}
function rungeKutta(x0, y0, x, h)
{
let n = ((x - x0) / h);
let k1, k2;
let y = y0;
for (let i = 1; i <= n; i++) {
k1 = h * dydx(x0, y);
k2 = h * dydx(x0 + 0.5 * h,
y + 0.5 * k1);
y = y + (1.0 / 6.0) * (k1 + 2 * k2);
x0 = x0 + h;
}
return y;
}
let x0 = 0, y = 1,
x = 2, h = 0.2;
document.write(rungeKutta(x0, y, x, h).toFixed(6));
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...