RTL (Register Transfer Level) design vs Sequential logic design
Last Updated :
21 Dec, 2018
In this article we try to explain the fundamental differences between Register Transfer Level (RTL) Design and Sequential Logic Design.
In the
RTL Design methodology different types of registers such as Counters, Shift Register, SIPO (Serial In Parallel Out), PISO (Parallel In Serial Out) are used as the basic building blocks for any Sequential Logic Circuits.
On the other hand
Synchronous Sequential Logic Design methodology different logic gates and different memory elements such as flip flops (to store the state of circuit at any time) is used as the basic building blocks for sequential logic circuits.
The Synchronous Sequential Logic Design Process using state diagram and its shortcomings are explained in the following example:
Lets say, we are to design a 2-bit synchronous Binary Up Counter whose count sequence is:
00 -> 01 -> 10 -> 11 -> 00 -> 01 -> ..... so on.
- Step-1: In the 1st step we draw a State Diagram representing the above sequential circuit.
The State Diagram representing the above counter is shown below:
 Figure – State Diagram for 2-bit UP Counter
Figure – State Diagram for 2-bit UP Counter
- Step-2: In the next step we derive the State Table from the above given State Diagram
The State Table is as given below:
| Present State Q(n) |
Next State Q(n+1) |
Output |
| 00 |
01 |
01 |
| 01 |
10 |
10 |
| 10 |
11 |
11 |
| 11 |
00 |
00 |
- Step-3: In the third step we need to choose the type of flip flop we will be using to store the state of the circuit, for simplicity, we will be considering the Positive Edge Triggered D-type Flip-Flop.We also need to determine the number of Flip-Flops required to represent the internal state of the circuit. The general formula for the number of Flip-Flops required:
Total Number of Flip-Flops = 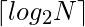 Where,
N = Total Number of States in State Table
Where,
N = Total Number of States in State Table
Then we need to note down the Excitation Table for chosen Flip-Flop. The Excitation Table for the D-type Flip-Flop is shown below:
| Present State Q(n) |
Next State Q(n+1) |
D |
| X |
0 |
0 |
| X |
1 |
1 |
- Step-4: In this step we combine the State Table from the 2nd step with the excitation table of the previous step as follows:
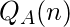 |
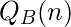 |
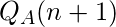 |
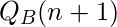 |
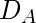 |
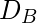 |
| 0 |
0 |
0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
0 |
1 |
0 |
| 1 |
0 |
1 |
1 |
1 |
1 |
| 1 |
1 |
0 |
0 |
0 |
0 |
- Step-5: Next, from the above table we try to express
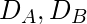 as boolean functions of
as boolean functions of 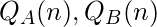 .
In this case the expression for both
.
In this case the expression for both 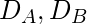 are trivial.
are trivial.

The Final Sequential Circuit is shown below:
 Figure – The Final Circuit
Figure – The Final Circuit
Shortcomings of the above process:
- From the above example we observe that the Synchronous Sequential Logic Design process is a fairly involved process and requires us to go through a sequence of well defined steps even for simple circuits like the one above.
- Secondly, if the number of states become large then this process becomes cumbersome and time-consuming, and sometimes even impossible.
To Address the above drawbacks of the Sequential Logic Design process and to enable Digital Designers to design circuits of higher complexity with ease, the
RTL design methodology was introduced. The most popular example of RTL Design is that of a Processor, which is nothing but a very sophisticated
Finite State Machine with a very large number of states.
The
main differences between RTL Design and Sequential Logic Design are summarized below:
| RTL Design |
Sequential Logic Design |
| In RTL Design the basic building blocks are registers, Multiplexers, Adders. |
In Sequential Logic Design the basic building blocks are the Logic Gates, Flip-Flops. |
| RTL Design is much closer to the Behavioural Design of a Logic Circuit as it models the data flow among different registers, and hence is much more intuitive. |
Sequential Logic Design process is more mechanical in nature as compared to RTL design process |
| Finally, RTL Modelling allows us to synthesize complex circuits with a large number of States with much more ease as compared to Sequential Logic Design. |
The Sequential Logic Design techniques are only applicable to circuits having a small number of states. |
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...