Root Locus using MATLAB
Last Updated :
20 Aug, 2020
In control systems, root locus analysis is a graphical strategy for looking at how the foundations of a system change with variety of a specific system boundary, generally an addition inside a feedback system.
Purpose of root locus in control system are as follows:
- To find the stability
- To check a point is on root locus or not
- To find system gain i.e. “k” or system parameter
Construction rules of a root locus :
Rule 1: A point will exists on real axis, root locus branches if the sum of poles and zeros to the right hand side of the point must be odd.
Rule 2: Asymptotes: They are root locus branches which starts on real axis and approaches to infinity.
Number of asymptotes “N = P – Z”
Here “P” is number of poles and “Z” is number of zeros
Rule 3: Angle of Asymptotes
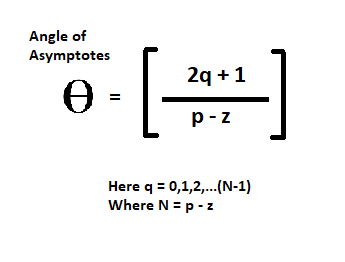
Rule 4: Centroid : Meeting point of asymptotes on real axis is called as centroid
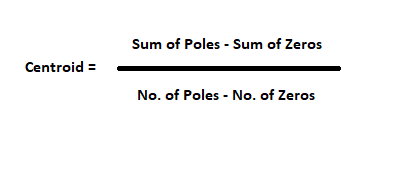
Rule 5: Break Point (BP): There are two types
- Break Away Point (BAP)
- Break In Point (BIP)
Rule 6: Root locus intersection point (IP) with imaginary axis.
Rule 7:
a) Angle of departure: It is calculated for complex conjugated poles or imaginary poles
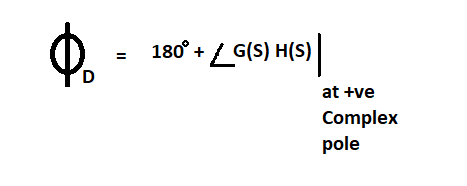
b) Angle of arrival: It is calculated for complex conjugate zeros or imaginary zeros
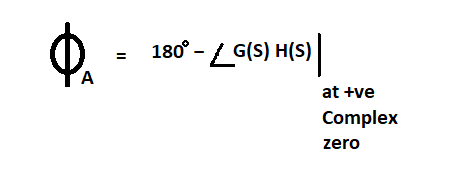
Code :
NUM = [1 10];
DEN = [1 6 8 0];
poly1 = [1 2];
poly2 = [1 4];
poly = conv(poly1, poly2);
roots(DEN);
sys = tf(NUM, DEN);
rltool(sys);
|
Output :


Share your thoughts in the comments
Please Login to comment...