Reversing the first K elements of a Queue
Last Updated :
13 Apr, 2023
Given an integer k and a queue of integers, The task is to reverse the order of the first k elements of the queue, leaving the other elements in the same relative order.
Only following standard operations are allowed on queue.
- enqueue(x) : Add an item x to rear of queue
- dequeue() : Remove an item from front of queue
- size() : Returns number of elements in queue.
- front() : Finds front item.
Approach:
We can use recursive call stack and we can add remaining items of front without using additional queue.
Below are the steps:
1. Reverse first k elements.
2. Remove from front and add to back (N – K) elements.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void solve(queue<int>& q, int k);
queue<int> reverseFirstK(queue<int> q, int k) {
solve(q, k);
int s = q.size() - k;
while (s-- > 0) {
int x = q.front();
q.pop();
q.push(x);
}
return q;
}
void solve(queue<int>& q, int k) {
if (k == 0) return;
int e = q.front();
q.pop();
solve(q, k - 1);
q.push(e);
}
int main() {
queue<int> queue;
queue.push(10);
queue.push(20);
queue.push(30);
queue.push(40);
queue.push(50);
queue.push(60);
queue.push(70);
queue.push(80);
queue.push(90);
queue.push(100);
int k = 5;
queue = reverseFirstK(queue, k);
while (!queue.empty()) {
cout << queue.front() << " ";
queue.pop();
}
return 0;
}
|
Java
import java.io.*;
import java.util.*;
public class GFG {
static Queue<Integer> reverseFirstK(Queue<Integer> q, int k) {
solve(q, k);
int s = q.size() - k;
while( s-- > 0){
int x = q.poll();
q.add(x);
}
return q;
}
static void solve(Queue<Integer> q, int k){
if(k == 0) return;
int e = q.poll();
solve(q, k - 1);
q.add(e);
}
public static void main (String[] args) {
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(10);
queue.add(20);
queue.add(30);
queue.add(40);
queue.add(50);
queue.add(60);
queue.add(70);
queue.add(80);
queue.add(90);
queue.add(100);
int k = 5;
queue = reverseFirstK(queue, k);
while (!queue.isEmpty()) {
System.out.print(queue.poll() + " ");
}
}
}
|
Python3
from collections import deque
def reverse_first_k(q, k):
solve(q, k)
s = len(q) - k
for _ in range(s):
x = q.popleft()
q.append(x)
return q
def solve(q, k):
if k == 0:
return
e = q.popleft()
solve(q, k - 1)
q.append(e)
queue = deque([10, 20, 30, 40, 50, 60, 70, 80, 90, 100])
k = 5
queue = reverse_first_k(queue, k)
while queue:
print(queue.popleft(), end=' ')
|
C#
using System;
using System.Collections.Generic;
class GFG {
public static LinkedList<int> queue;
public static void solve(int k) {
if (k == 0){
return;
}
int e = queue.First.Value;
queue.RemoveFirst();
solve(k - 1);
queue.AddLast(e);
}
public static void reverseFirstK(int k) {
solve(k);
int s = queue.Count - k;
while (s > 0) {
int x = queue.First.Value;
queue.RemoveFirst();
queue.AddLast(x);
s = s - 1;
}
}
public static void Main(string[] args) {
queue = new LinkedList<int>();
queue.AddLast(10);
queue.AddLast(20);
queue.AddLast(30);
queue.AddLast(40);
queue.AddLast(50);
queue.AddLast(60);
queue.AddLast(70);
queue.AddLast(80);
queue.AddLast(90);
queue.AddLast(100);
int k = 5;
reverseFirstK(k);
while (queue.Count > 0)
{
Console.Write(queue.First.Value + " ");
queue.RemoveFirst();
}
}
}
|
Javascript
class Queue {
constructor() {
this.items = [];
}
push(element) {
return this.items.push(element);
}
pop() {
if (this.items.length > 0) {
return this.items.shift();
}
}
front() {
return this.items[0];
}
isEmpty() {
return this.items.length == 0;
}
size() {
return this.items.length;
}
}
function reverseFirstK(queue, k) {
solve(queue, k);
let s = queue.size() - k;
while (s-- > 0) {
let x = queue.front();
queue.pop();
queue.push(x);
}
return queue;
}
function solve(queue, k) {
if (k == 0) return;
let e = queue.front();
queue.pop();
solve(queue, k - 1);
queue.push(e);
}
let queue = new Queue();
queue.push(10);
queue.push(20);
queue.push(30);
queue.push(40);
queue.push(50);
queue.push(60);
queue.push(70);
queue.push(80);
queue.push(90);
queue.push(100);
let k = 5;
q = reverseFirstK(queue, k);
while (!q.isEmpty()) {
console.log(q.front());
q.pop();
}
|
Output50 40 30 20 10 60 70 80 90 100
Time and Space complexity:
The time complexity of the given program can be analyzed as follows:
The function reverseFirstK calls the recursive function solve, which takes O(k) time to reverse the first k elements of the queue.
The remaining part of the function reverseFirstK takes O(n-k) time to move the remaining elements to the end of the queue.
The overall time complexity of the function reverseFirstK is O(n), where n is the size of the input queue.
Therefore, the time complexity of the entire program is O(n).
The space complexity of the program is also O(n), as the input queue is stored in memory along with some additional variables used in the program, such as the integer variable s. However, the space used by the recursive function solve is O(k), as it calls itself recursively k times, where k is the number of elements to be reversed.
Therefore, the overall space complexity of the program is O(n+k).
Approach:
The idea is to use an auxiliary stack. Store the first k elements of the queue in a stack and pop it from the queue, then push it back to the queue and perform pop operation for n-k times and again push the popped element.
Follow the below steps to implement the idea:
- Create an empty stack.
- One by one dequeue first K items from given queue and push the dequeued items to stack.
- Enqueue the contents of stack at the back of the queue
- Dequeue (size-k) elements from the front and enqueue them one by one to the same queue.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void reverseQueueFirstKElements(int k, queue<int>& Queue)
{
if (Queue.empty() == true || k > Queue.size())
return;
if (k <= 0)
return;
stack<int> Stack;
for (int i = 0; i < k; i++) {
Stack.push(Queue.front());
Queue.pop();
}
while (!Stack.empty()) {
Queue.push(Stack.top());
Stack.pop();
}
for (int i = 0; i < Queue.size() - k; i++) {
Queue.push(Queue.front());
Queue.pop();
}
}
void Print(queue<int>& Queue)
{
while (!Queue.empty()) {
cout << Queue.front() << " ";
Queue.pop();
}
}
int main()
{
queue<int> Queue;
Queue.push(10);
Queue.push(20);
Queue.push(30);
Queue.push(40);
Queue.push(50);
Queue.push(60);
Queue.push(70);
Queue.push(80);
Queue.push(90);
Queue.push(100);
int k = 5;
reverseQueueFirstKElements(k, Queue);
Print(Queue);
}
|
Java
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class Reverse_k_element_queue {
static Queue<Integer> queue;
static void reverseQueueFirstKElements(int k)
{
if (queue.isEmpty() == true || k > queue.size())
return;
if (k <= 0)
return;
Stack<Integer> stack = new Stack<Integer>();
for (int i = 0; i < k; i++) {
stack.push(queue.peek());
queue.remove();
}
while (!stack.empty()) {
queue.add(stack.peek());
stack.pop();
}
for (int i = 0; i < queue.size() - k; i++) {
queue.add(queue.peek());
queue.remove();
}
}
static void Print()
{
while (!queue.isEmpty()) {
System.out.print(queue.peek() + " ");
queue.remove();
}
}
public static void main(String args[])
{
queue = new LinkedList<Integer>();
queue.add(10);
queue.add(20);
queue.add(30);
queue.add(40);
queue.add(50);
queue.add(60);
queue.add(70);
queue.add(80);
queue.add(90);
queue.add(100);
int k = 5;
reverseQueueFirstKElements(k);
Print();
}
}
|
Python3
from queue import Queue
def reverseQueueFirstKElements(k, Queue):
if (Queue.empty() == True or
k > Queue.qsize()):
return
if (k <= 0):
return
Stack = []
for i in range(k):
Stack.append(Queue.queue[0])
Queue.get()
while (len(Stack) != 0):
Queue.put(Stack[-1])
Stack.pop()
for i in range(Queue.qsize() - k):
Queue.put(Queue.queue[0])
Queue.get()
def Print(Queue):
while (not Queue.empty()):
print(Queue.queue[0], end=" ")
Queue.get()
if __name__ == '__main__':
Queue = Queue()
Queue.put(10)
Queue.put(20)
Queue.put(30)
Queue.put(40)
Queue.put(50)
Queue.put(60)
Queue.put(70)
Queue.put(80)
Queue.put(90)
Queue.put(100)
k = 5
reverseQueueFirstKElements(k, Queue)
Print(Queue)
|
C#
using System;
using System.Collections.Generic;
class GFG {
public static LinkedList<int> queue;
public static void reverseQueueFirstKElements(int k)
{
if (queue.Count == 0 || k > queue.Count) {
return;
}
if (k <= 0) {
return;
}
Stack<int> stack = new Stack<int>();
for (int i = 0; i < k; i++) {
stack.Push(queue.First.Value);
queue.RemoveFirst();
}
while (stack.Count > 0) {
queue.AddLast(stack.Peek());
stack.Pop();
}
for (int i = 0; i < queue.Count - k; i++) {
queue.AddLast(queue.First.Value);
queue.RemoveFirst();
}
}
public static void Print()
{
while (queue.Count > 0) {
Console.Write(queue.First.Value + " ");
queue.RemoveFirst();
}
}
public static void Main(string[] args)
{
queue = new LinkedList<int>();
queue.AddLast(10);
queue.AddLast(20);
queue.AddLast(30);
queue.AddLast(40);
queue.AddLast(50);
queue.AddLast(60);
queue.AddLast(70);
queue.AddLast(80);
queue.AddLast(90);
queue.AddLast(100);
int k = 5;
reverseQueueFirstKElements(k);
Print();
}
}
|
Javascript
<script>
function reverseQueueFirstKElements(k,Queue)
{
if (Queue.length == 0 || k > Queue.length)
return;
if (k <= 0)
return;
let Stack = [];
for (let i = 0; i < k; i++) {
Stack.push(Queue.shift());
}
while (Stack.length > 0) {
Queue.push(Stack.pop());
}
for (let i = 0; i < Queue.length - k; i++) {
Queue.push(Queue.shift());
}
}
function Print(Queue)
{
while (Queue.length > 0) {
document.write(Queue.shift()," ");
}
}
let Queue = [];
Queue.push(10);
Queue.push(20);
Queue.push(30);
Queue.push(40);
Queue.push(50);
Queue.push(60);
Queue.push(70);
Queue.push(80);
Queue.push(90);
Queue.push(100);
let k = 5;
reverseQueueFirstKElements(k, Queue);
Print(Queue);
</script>
|
Output50 40 30 20 10 60 70 80 90 100
Time Complexity: O(N + k), Where ‘n’ is the total number of elements in the queue and ‘k’ is the number of elements to be reversed. This is because firstly the whole queue is emptied into the stack and after that first ‘k’ elements are emptied and enqueued in the same way.
Auxiliary Space: O(k) where k is no of elements to be reversed since stack is being used to store values for the purpose of reversing.
Using Doubly Ended Queue:
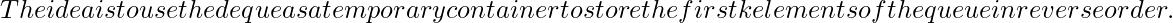
Follow the steps below to implement the above idea:
- Dequeue the first k elements of the queue and push them onto a deque using the push_front() function.
- Pop the elements from the deque one by one using the pop_front() function and enqueue them back into the queue using the push() function.
- Dequeue the remaining elements from the queue and enqueue them back into the queue using the push() and pop() functions.
Below is the implementation of the above approach:
C++
#include <deque>
#include <iostream>
#include <queue>
using namespace std;
void reverseFirstK(queue<int>& q, int k)
{
deque<int> d;
for (int i = 0; i < k; i++) {
d.push_front(q.front());
q.pop();
}
while (!d.empty()) {
q.push(d.front());
d.pop_front();
}
for (int i = 0; i < q.size() - k; i++) {
q.push(q.front());
q.pop();
}
}
int main()
{
queue<int> q;
q.push(10);
q.push(20);
q.push(30);
q.push(40);
q.push(50);
q.push(60);
q.push(70);
q.push(80);
q.push(90);
q.push(100);
int k = 5;
reverseFirstK(q, k);
while (!q.empty()) {
cout << q.front() << " ";
q.pop();
}
return 0;
}
|
Java
import java.util.*;
public class ReverseFirstKQueue {
public static void reverseFirstK(Queue<Integer> q, int k){
Deque<Integer> d = new ArrayDeque<>();
for (int i = 0; i < k; i++) {
d.push(q.poll());
}
while (!d.isEmpty()) {
q.add(d.pop());
}
for (int i = 0; i < q.size() - k; i++) {
q.add(q.poll());
}
}
public static void main(String[] args){
Queue<Integer> q = new LinkedList<Integer>();
q.add(10);
q.add(20);
q.add(30);
q.add(40);
q.add(50);
q.add(60);
q.add(70);
q.add(80);
q.add(90);
q.add(100);
int k = 5;
reverseFirstK(q, k);
while (!q.isEmpty()) {
System.out.print(q.peek() + " ");
q.poll();
}
}
}
|
Python3
from collections import deque
def reverseFirstK(q, k):
d = deque()
for i in range(k):
d.appendleft(q.popleft())
while d:
q.append(d.popleft())
for i in range(len(q) - k):
q.append(q.popleft())
q = deque()
q.append(10)
q.append(20)
q.append(30)
q.append(40)
q.append(50)
q.append(60)
q.append(70)
q.append(80)
q.append(90)
q.append(100)
k = 5
reverseFirstK(q, k)
print(*q)
|
C#
using System;
using System.Collections.Generic;
public class ReverseFirstKQueue {
public static void reverseFirstK(Queue<int> q, int k){
Stack<int> s = new Stack<int>();
for (int i = 0; i < k; i++) {
s.Push(q.Dequeue());
}
while (s.Count > 0) {
q.Enqueue(s.Pop());
}
for (int i = 0; i < q.Count - k; i++) {
q.Enqueue(q.Dequeue());
}
}
public static void Main(){
Queue<int> q = new Queue<int>();
q.Enqueue(10);
q.Enqueue(20);
q.Enqueue(30);
q.Enqueue(40);
q.Enqueue(50);
q.Enqueue(60);
q.Enqueue(70);
q.Enqueue(80);
q.Enqueue(90);
q.Enqueue(100);
int k = 5;
reverseFirstK(q, k);
while (q.Count > 0) {
Console.Write(q.Peek() + " ");
q.Dequeue();
}
}
}
|
Javascript
function reverseFirstK(q, k) {
const d = [];
for (let i = 0; i < k; i++) {
d.unshift(q.shift());
}
while (d.length !== 0) {
q.push(d.shift());
}
for (let i = 0; i < q.length - k; i++) {
q.push(q.shift());
}
}
const q = [];
q.push(10);
q.push(20);
q.push(30);
q.push(40);
q.push(50);
q.push(60);
q.push(70);
q.push(80);
q.push(90);
q.push(100);
const k = 5;
reverseFirstK(q, k);
console.log(q.join(' '));
|
Output50 40 30 20 10 60 70 80 90 100
Time Complexity: O(n), The time complexity of this approach is O(n) where n is the total number of elements in the queue.
Auxiliary Space: O(k) , The space complexity of this approach is O(k) because we are using a deque to store the first k elements of the queue.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...