Reversing Deterministic Finite Automata
Last Updated :
12 Jan, 2022
Prerequisite – Designing finite automata
Reversal: We define the reversed language 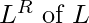 to be the language
to be the language 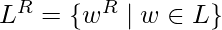 , where
, where 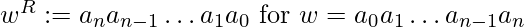
Steps to Reversal:
- Draw the states as it is.
- Add a new single accepting state
- Make the accepting state the initial state and initial state the accepting state
- Invert the transition function into a transition relation
- Remove any states that are no longer necessary
Note :
Reversing deterministic finite automaton results in a non-deterministic finite automaton. This can then be converted to a deterministic finite automaton by the conversion algorithm.
The reversal process goes like this:

Let’s understand the Reversal process in Deterministic Finite Automata (DFA) with the help of the example below.
Example 1:
We propose a deterministic finite automaton for the language of words beginning with the symbol ‘a’:
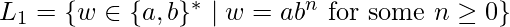
We can construct the following state transition diagram:

We now want to construct the finite automaton that will accept the reverse of this language, 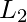 .
.
First, we add a new single accepting state. This is because eventually we will need to swap the accepting and initial states, and there can only be a single initial state.

Then, switch the initial and accepting states:

Invert the transition function into a transition relation:

Whilst this is a valid solution, the node marked as C is dangling since it has no incident edges. Therefore it can be removed to give a clean, final result:

This resulting finite automaton is a non-deterministic finite automaton. Therefore the resulting reversed language is regular.
Explanation:
- Same states (A, B, C) are drawn as present in an original state diagram
- Since A is the initial state make it the final state.
- Since B is the final state make it the initial state.
- Reversing the edges, since previously edges point A to B and A to C . Change the direction, now edges points toward B to A and C to A.
- Assign the values as same as the original.
- Draw the loop as in the original state diagram
- Since there is no incident edge on state C so, we can reduce this state C.
- Since there is no transition for ‘a’ and ‘b’ in state A . Therefore resultant FA is NFA.
Example-2:
Designing a DFA for the set of strings over {a, b} such that string of the language contains an even number of ‘a’. The desired language will be formed:
L1 = { , aa, aab, aba, aab, aababa, .......}
, aa, aab, aba, aab, aababa, .......}
In L1, each string has an even number of elements a.
State Transition Diagram for the language L1:

This DFA accepts all the strings containing an even number of elements a. Here, State A is the initial state, and state A is the final state. Now, Reversing the L1 language which gives the final result of the language L2.
State Transition Diagram of L2 (reverse of L1):

Thus as we see that L2 has been obtained through the reversal process and this final DFA accepts all the strings containing an even number of element a which is the same as the original language.
L2 = { , aa, aab, aba, aab, aababa, .......}
, aa, aab, aba, aab, aababa, .......}
Explanation:
- Same states (A, B) are drawn as present in an original state diagram.
- Since A is the initial state make it the final state.
- Since A is the final state make it the initial state.
- Reversing the edges, since previously edges point A to B and so on. Change the direction, now edges points toward B to A and so on.
- Assign the values as same as the original.
- Since there is a transition for ‘a’ and ‘b’ in states A and B.Therefore resultant FA is DFA.
- Since the State diagram after and before the reversal is the same. Therefore L1 = L2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...