Resolution Algorithm in Artificial Intelligence
Last Updated :
27 May, 2022
Prerequisite:
Inference algorithms based on resolution work utilize the proof-by-contradiction. To establish that is 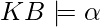 unsatisfiable, we show that
unsatisfiable, we show that 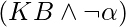 is unsatisfiable. We do this by demonstrating a contradiction.
is unsatisfiable. We do this by demonstrating a contradiction.

The equations above show a resolution algorithm. To begin, 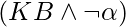 is transformed to CNF. The resolution rule is then applied to the clauses that result. Each pair of complementary literals is resolved into a new clause, which is added to the set if it does not exist before. The procedure continues until either
is transformed to CNF. The resolution rule is then applied to the clauses that result. Each pair of complementary literals is resolved into a new clause, which is added to the set if it does not exist before. The procedure continues until either
- no more clauses can be added, in which case, KB does not entail
- two clauses resolve to produce the empty clause, in which case KB entails.
Because a disjunction is true only if at least one of its disjunctions is true, the empty clause—a disjunction with no disjunctions—is identical to False. Another approach to recognize that an empty sentence is a contradiction is to notice that it only appears when two complementary unit clauses, such as 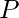 and
and 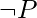 , are resolved.
, are resolved.
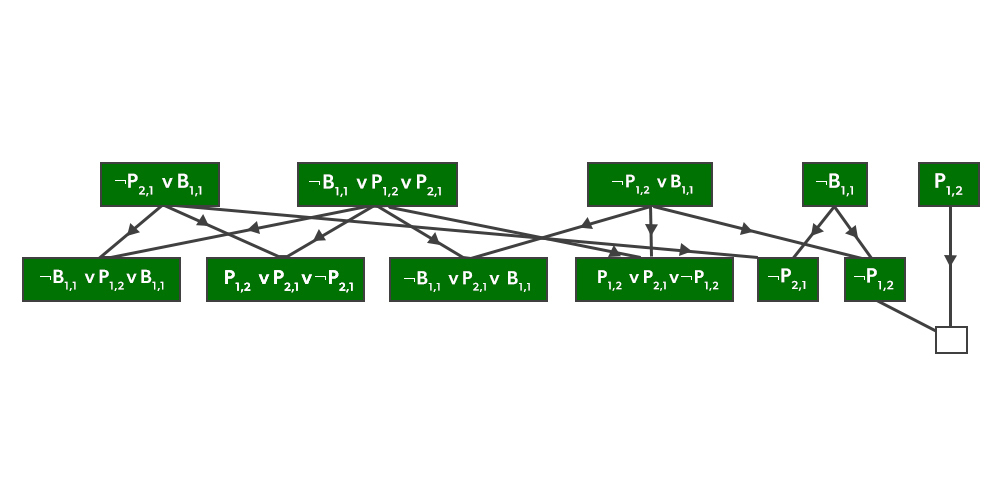
In the wumpus universe, we may use the resolution technique to solve a very easy inference. There is no breeze when the agent is in [1,1], hence no pits may form in nearby squares. 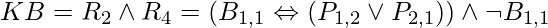 is the appropriate knowledge base, and we want to verify
is the appropriate knowledge base, and we want to verify 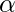 which is, say,
which is, say, 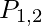 . The clauses presented in the above figure are obtained by converting
. The clauses presented in the above figure are obtained by converting 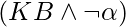 into CNF. Clauses derived by resolving couples in the first row are shown in the second row of the picture. The empty clause, depicted as a little square, is obtained when
into CNF. Clauses derived by resolving couples in the first row are shown in the second row of the picture. The empty clause, depicted as a little square, is obtained when 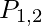 is resolved with
is resolved with 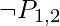 . The figure above illustrates that many of the resolution stages are unnecessary. For example, the phrase
. The figure above illustrates that many of the resolution stages are unnecessary. For example, the phrase 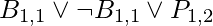 is identical to
is identical to 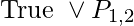 which is equivalent to
which is equivalent to 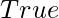 . It’s not particularly useful to deduce that
. It’s not particularly useful to deduce that 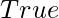 is true. As a result, any phrase containing two complementing literals can be removed.
is true. As a result, any phrase containing two complementing literals can be removed.
Share your thoughts in the comments
Please Login to comment...