Representation of Rational Numbers on the Number Line | Class 8 Maths
Last Updated :
17 Feb, 2021
Rational numbers are the integers p and q expressed in the form of p/q where q>0. Rational numbers can be positive, negative or even zero. Rational numbers can be depicted on the number line. The centre of the number line is called Origin (O). Positive rational numbers are illustrated on the right side of zero (called origin), and negative on left side of origin. The representation of rational numbers on the number line depends on the type of fraction.
Proper Fractions
Given a fraction p/q, a proper fraction has p<q, and therefore p/q < 1 always. Also, p/q can never be zero.
Positive proper fractions, therefore, will always lie between 0 and 1 on the number line. Negative will lie on the left side of the origin, between 0 and -1.
Examples for Proper Fractions on Number Line
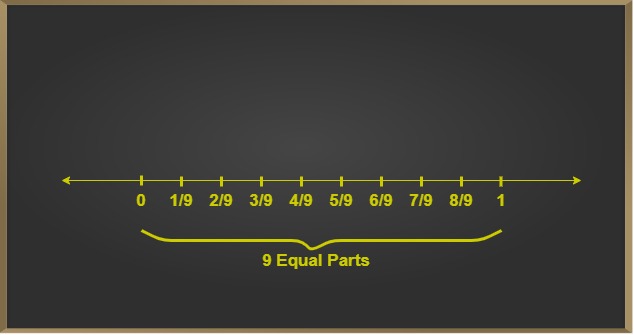
Example 1: Representation of 5/9 on the number line.
Solution:
- First, we mark the origin and integer value 1 on the number line, since proper rational numbers lie between 0 and 1.
- Next, we divide this region into equal parts, such that these parts are equal to the denominator value.
- Then, we mark the part with the value equal to the numerator.
Example 2: Representation of -3/4 on the number line.
Solution:
- First, we mark the origin and integer value -1 on the number line, since proper rational numbers lie between 0 and -1.
- Next, we divide this region into 4 equal parts.
- To mark -3, move three parts on the left-side of zero.
4

Example 3: Representation of 1/11 on the number line
Solution:
- First, we mark the origin and integer value 1 on the number line, since proper rational numbers lie between 0 and 1.
- Next, we divide this region into 11 equal parts.
- To mark 1/11, move one part on the right-side of zero.

Improper Fractions
Given an improper fraction p/q, the numerator (p) > denomination (q), such that the ratio p/q>1. Improper fractions are first converted into mixed fractions, that is, 11/2 ⇢ 51/2, here 5 is whole number part, 1/2 is fraction part.
Examples for Improper Fractions on Number Line
Example 1: Represent 95/4 on a number line.
Solution:
Converting to a mixed fraction we get, 233
4
The mixed fraction is then plotted on the number line, which lies in the range of the whole number part and whole number part +1. This region is then divided into equal parts, corresponding to the denominator of the fraction part and marking the pth (that is, numerator) part.
95 ⇒ 23 3
4 4
Step 1:

Step 2:

Step 3:

Example 2: Represent -5 on a number line
3
Solution:
Converting to a mixed fraction we get -5 ⇒ -1-2
3 3
Here -1 is the whole number part, – 2 is the fraction part
3
The mixed fraction is then plotted on the number line, which lies in the range of the whole number part and whole number part +1. This region is then divided into equal parts, corresponding to the denominator of the fraction part and marking the pth (that is, numerator) part.
-5 ⇒ -1-2
3 3

In the case of negative fractions, we move towards the origin.
Example 3: Represent 5 on a number line.
2
Solution:
Converting to a mixed fraction we get 5 ⇒ 21
2 2
Here 1 is the whole number part, 1 is fraction part
2
The mixed fractions is then plotted on the number line, which lies in the range of the whole number part and whole number part + 1, which is 1 and 2 in this case. This region is then divided into equal parts, corresponding to the denominator of the fraction part and marking the numerator part. That is marking 1st out of 2 parts on the number line.

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...