Representation of Negative Binary Numbers
Last Updated :
22 Apr, 2020
Since binary numbers can have only two symbols either 0 or 1 for each position or bit, so it is not possible to add minus or plus symbols in front of a binary number.
We represent negative binary numbers using a minus symbol in front of them. In computer number representation, these numbers can be distinguishable with the help of an extra bit or flag called sign bit or sign flag in the Binary number representation system for signed numbers. This extra bit is called sign bit or sign flag which has a value of sign bit is 0 for positive numbers and 1 for negative binary numbers.
The representation of magnitude of positive numbers is easy and does not need any changes.
The representation of magnitude of negative numbers is changed accordingly to represent it.
Ways to represent magnitudes :
These are: Sign-Magnitude method, 1’s Complement method, and 2’s complement method. These are explained as follows using examples.
- Signed Magnitude Method :
We only add an extra sign bit to recognize negative and positive numbers. Sign bit has 1 for negative number and 0 for positive number.

Range of Numbers :
For n bits register, MSB will be sign bit and (n-1) bits will be magnitude. Then,
Negative lowest number that can be stored is -(2(k-1)-1)and positive largest number that can be stored is (2(k-1)-1) .
But, this (sign) representation has an ambiguous representation of number 0. It means 0 has two different representation one is -0 (e.g., 1 00000 in six bit register) and second is +0 (e.g., 0 00000 in six bit register).

- 1’s Complement Method :
Please note that MSB is always Sign bit, if it 0, then there are no changes. MSB is always 1 in case of negative numbers. We only take 1’s complement of negative numbers to represent in the computer.

Range of Numbers :
For n bits register, negative lowest number that can be stored is -(2(n-1)-1) and positive largest number that can be stored is (2(n-1)-1) .
But, this (sign) representation has an ambiguous representation of number 0. It means 0 has two different representations one is -0 (e.g., 1 1111 in five bit register) and second is +0 (e.g., 0 0000 in five bit register).

- 2’s Complement Method :
Please note that MSB is always Sign bit, if it 0, then there are no changes. MSB is always 1 in case of negative numbers. We only take 2’s complement of negative numbers to represent in the computer.
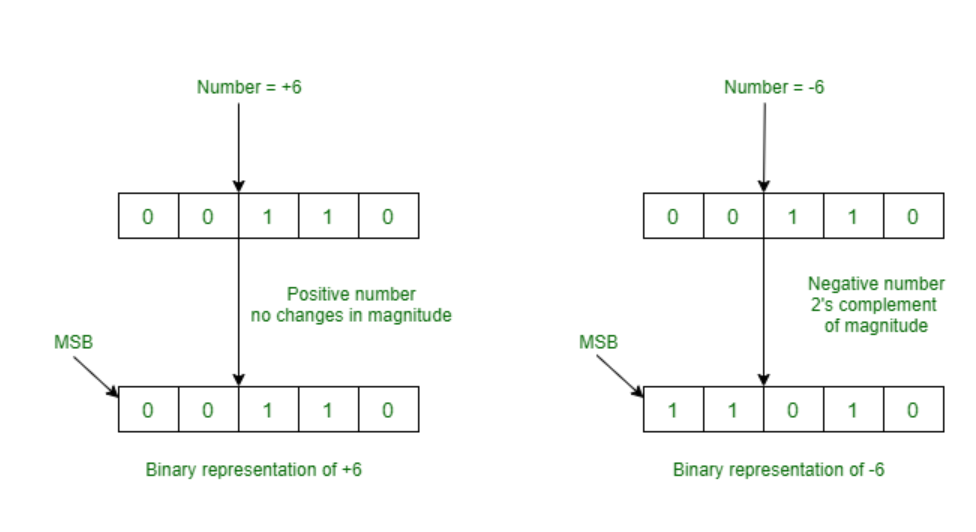
Since, there is only one representation of +0 and -0, so this 2’s complement representation is better than sign representation and 1’s complement representation.

Range of Numbers :
For n bits register, negative lowest number that can be stored is -(2(n-1)) and positive largest number that can be stored is (2(n-1)-1) .
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...