Represent a number as a sum of maximum possible number of Prime Numbers

Given a positive integer 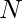. The task is to represent it as a sum of the maximum possible number of prime numbers. (N > 1)
Examples: 

Input : N = 5 
Output : 2 3 

Input : N = 6
Output : 2 2 2

At first, the problem might seem to involve some use of Goldbach’s conjecture. But the key observation here is to maximise the number of terms used, you should use as small numbers as possible. This leads to the following idea: 

• If N is even, it can be represented as sum of 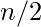two’s.
• Otherwise, 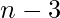has to be even and hence N can be represented as sum of one 3 and 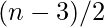two’s. 
  

This is the maximum number of primes whose sum is N.
Below is the implementation of the above approach: 

C++

// CPP program to represent a number as a
// sum of maximum possible number of
// Prime Numbers
#include <bits/stdc++.h>
using namespace std;

// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
void printAsMaximalPrimeSum(int n)
{
    // If n is odd, print one 3
    if (n % 2 == 1) {
        cout << "3 ";
        n -= 3;
    }

    // Now n is even, print 2 n/2 times
    while (n) {
        cout << "2 ";
        n -= 2;
    }
}

// Driver Code
int main()
{
    int n = 5;
    printAsMaximalPrimeSum(n);
}

Java

// Java program to represent a number as a
// sum of maximum possible number of
// Prime Numbers

import java.io.*;

class GFG {

// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
static void printAsMaximalPrimeSum(int n)
{
    // If n is odd, print one 3
    if (n % 2 == 1) {
        System.out.print( "3 ");
        n -= 3;
    }

    // Now n is even, print 2 n/2 times
    while (n>0) {
        System.out.print( "2 ");
        n -= 2;
    }
}

       // Driver Code
    public static void main (String[] args) {
    int n = 5;
    printAsMaximalPrimeSum(n);
    }
}

// This Code is contributed by inder_verma..

Python3

# Python3 program to represent a number as a
# sum of maximum possible number of
# Prime Numbers


# Function to represent a number as a
# sum of the maximum possible number
# of Prime Numbers
def printAsMaximalPrimeSum( n):

    # If n is odd, print one 3
    if ( n % 2 == 1):
        print("3 ",end="")
        n -= 3


    # Now n is even, print 2 n/2 times
    while ( n>0):
        print("2 ",end="")
        n -= 2



# Driver Code

n = 5
printAsMaximalPrimeSum( n)

# This code is contributed by ihritik

C#

// C# program to represent a number as a
// sum of maximum possible number of
// Prime Numbers


using System;
class GFG
{
    // Function to represent a number as a
    // sum of the maximum possible number
    // of Prime Numbers
    static void printAsMaximalPrimeSum(int n)
    {
        // If n is odd, print one 3
        if (n % 2 == 1) {
            Console.Write("3 ");
            n -= 3;
        }

        // Now n is even, print 2 n/2 times
        while (n>0) {
            Console.Write("2 ");
            n -= 2;
        }
    }

    // Driver Code
    public static void Main()
    {
        int n = 5;
        printAsMaximalPrimeSum(n);
    }

}

// This code is contributed by ihritik

PHP

<?php
// PHP program to represent a number as a
// sum of maximum possible number of
// Prime Numbers


// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
function printAsMaximalPrimeSum($n)
{
    // If n is odd, print one 3
    if ($n % 2 == 1) {
        echo "3 ";
        $n -= 3;
    }

    // Now n is even, print 2 n/2 times
    while ($n>0) {
        echo "2 ";
        $n -= 2;
    }
}

// Driver Code

$n = 5;
printAsMaximalPrimeSum($n);


// This code is contributed by ihritik
?>

Javascript

<script>

// Javascript program to represent a number as a
// sum of maximum possible number of
// Prime Number

// Function to represent a number as a
// sum of the maximum possible number
// of Prime Numbers
function printAsMaximalPrimeSum(n)
{
    // If n is odd, print one 3
    if (n % 2 == 1) {
        document.write( "3 ");
        n -= 3;
    }

    // Now n is even, print 2 n/2 times
    while (n>0) {
        document.write( "2 ");
        n -= 2;
    }
}

// driver program

    let n = 5;
    printAsMaximalPrimeSum(n);

</script>

Output:

3 2

Time Complexity: O(N)