Removal of ambiguity (Converting an Ambiguous grammar into Unambiguous grammar)
Last Updated :
11 Jun, 2021
Prerequisites : Context Free Grammars , Ambiguous Grammar, Difference between ambiguous and unambiguous grammar, Precedence and Associativity of operators, Recursive Grammar
In this article we are going to see the removal of ambiguity from grammar using suitable examples.
Ambiguous vs Unambiguous Grammar :
The grammars which have more than one derivation tree or parse tree are ambiguous grammars. These grammar is not parsed by any parsers.
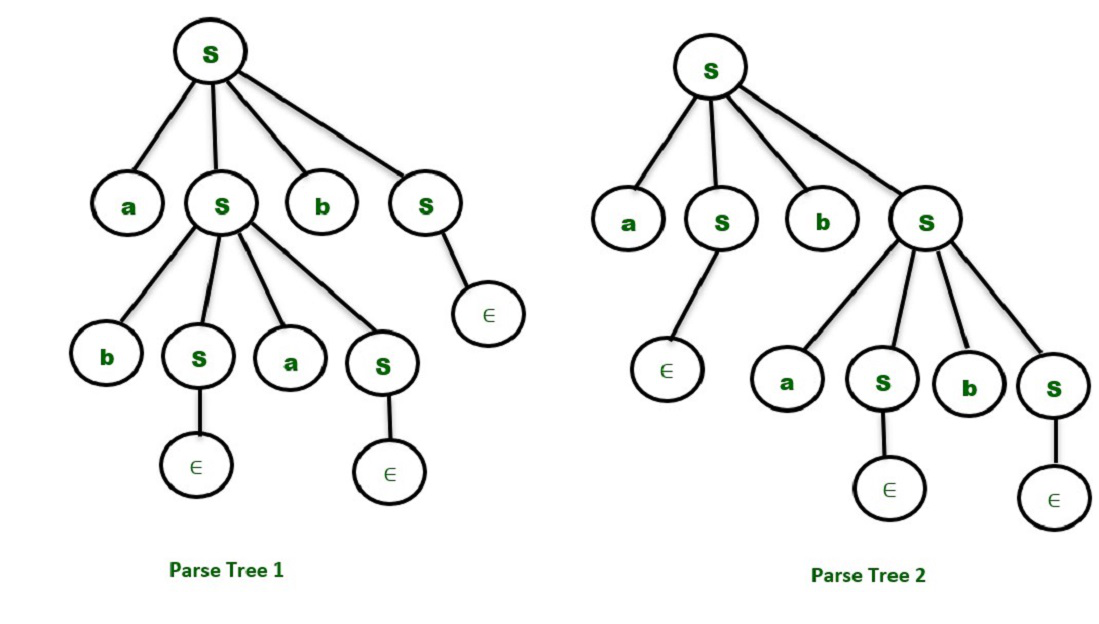
Example-
1. Consider the production shown below –
S->aSbS | bSaS | ∈
Say, we want to generate the string “abab” from the above grammar. We can observe that the given string can be derived using two parse trees. So, the above grammar is ambiguous.
The grammars which have only one derivation tree or parse tree are called unambiguous grammars.
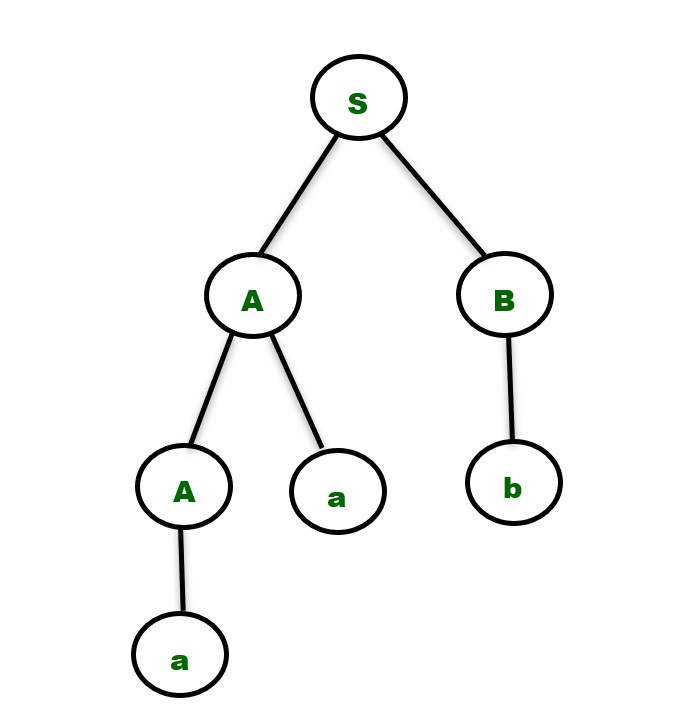
2. Consider the productions shown below –
S -> AB
A -> Aa | a
B -> b
For the string “aab” we have only one Parse Tree for the above grammar as shown below.
It is important to note that there are no direct algorithms to find whether grammar is ambiguous or not. We need to build the parse tree for a given input string that belongs to the language produced by the grammar and then decide whether the grammar is ambiguous or unambiguous based on the number of parse trees obtained as discussed above.
Note – The string has to be chosen carefully because there may be some strings available in the language produced by the unambiguous grammar which has only one parse tree.
Removal of Ambiguity :
We can remove ambiguity solely on the basis of the following two properties –
1. Precedence –
If different operators are used, we will consider the precedence of the operators. The three important characteristics are :
- The level at which the production is present denotes the priority of the operator used.
- The production at higher levels will have operators with less priority. In the parse tree, the nodes which are at top levels or close to the root node will contain the lower priority operators.
- The production at lower levels will have operators with higher priority. In the parse tree, the nodes which are at lower levels or close to the leaf nodes will contain the higher priority operators.
2. Associativity –
If the same precedence operators are in production, then we will have to consider the associativity.
- If the associativity is left to right, then we have to prompt a left recursion in the production. The parse tree will also be left recursive and grow on the left side.
+, -, *, / are left associative operators.
- If the associativity is right to left, then we have to prompt the right recursion in the productions. The parse tree will also be right recursive and grow on the right side.
^ is a right associative operator.
Example 1 – Consider the ambiguous grammar
E -> E-E | id
The language in the grammar will contain { id, id-id, id-id-id, ….}
Say, we want to derive the string id-id-id. Let’s consider a single value of id=3 to get more insights. The result should be :
3-3-3 =-3
Since the same priority operators, we need to consider associativity which is left to right.
Parse Tree – The parse tree which grows on the left side of the root will be the correct parse tree in order to make the grammar unambiguous.

So, to make the above grammar unambiguous, simply make the grammar Left Recursive by replacing the left most non-terminal E in the right side of the production with another random variable, say P. The grammar becomes :
E -> E – P | P
P -> id
The above grammar is now unambiguous and will contain only one Parse Tree for the above expression as shown below –

Similarly, the unambiguous grammar for the expression : 2^3^2 will be –
E -> P ^ E | P // Right Recursive as ^ is right associative.
P -> id
Example 2 – Consider the grammar shown below, which has two different operators :
E -> E + E | E * E | id
Clearly, the above grammar is ambiguous as we can draw two parse trees for the string “id+id*id” as shown below. Consider the expression :
3 + 2 * 5 // “*” has more priority than “+”
The correct answer is : (3+(2*5))=13

The “+” having the least priority has to be at the upper level and has to wait for the result produced by the “*” operator which is at the lower level. So, the first parse tree is the correct one and gives the same result as expected.
The unambiguous grammar will contain the productions having the highest priority operator (“*” in the example) at the lower level and vice versa. The associativity of both the operators are Left to Right. So, the unambiguous grammar has to be left recursive. The grammar will be :
E -> E + P // + is at higher level and left associative
E -> P
P -> P * Q // * is at lower level and left associative
P -> Q
Q -> id
(or)
E -> E + P | P
P -> P * Q | Q
Q -> id
E is used for doing addition operations and P is used to perform multiplication operations. They are independent and will maintain the precedence order in the parse tree.
The parse tree for the string ” id+id*id+id ” will be –
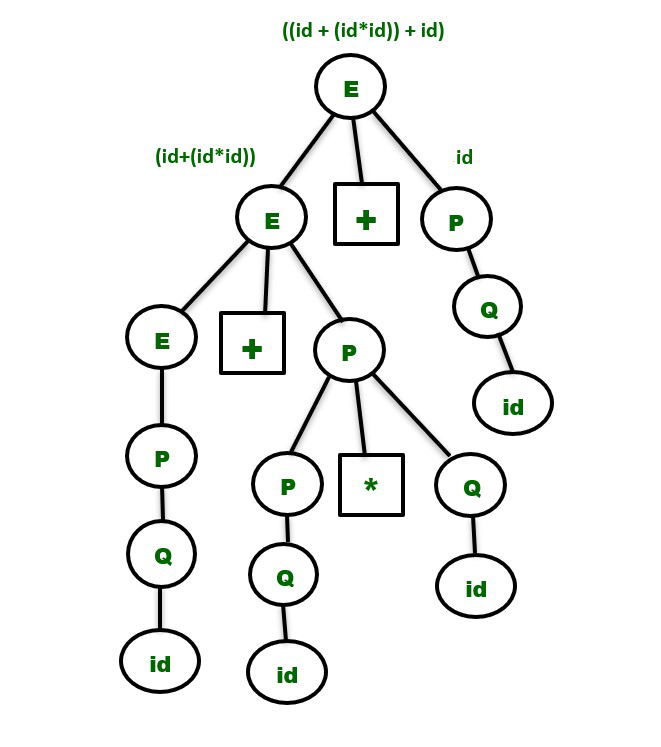
Note : It is very important to note that while converting an ambiguous grammar to an unambiguous grammar, we shouldn’t change the original language provided by the ambiguous grammar. So, the non-terminals in the ambiguous grammar have to be replaced with other variables in such a way that we get the same language as it was derived before and also maintain the precedence and associativity rule simultaneously.
This is the reason we wrote the production E -> P and P -> Q and Q -> id after replacing them in the above example, because the language contains the strings { id, id+id } as well.
Similarly, the unambiguous grammar for an expression having the operators -,*,^ is :
E -> E – P | P // Minus operator is at higher level due to least priority and left associative.
P -> P * Q | Q // Multiplication operator has more priority than – and lesser than ^ and left associative.
Q -> R ^ Q | R // Exponent operator is at lower level due to highest priority and right associative.
R -> id
Also, there are some ambiguous grammars which can’t be converted into unambiguous grammars.
Share your thoughts in the comments
Please Login to comment...