Relationship between TP, MP, and AP

Consumers and producers both play a crucial role in the efficient operation of an economy. A producer uses a variety of inputs to create commodities and services. Production is an essential economic activity since it transforms the product into the form consumers require, increasing its utility. It helps transform the raw materials into some desirable product. In simple words, it includes the transformation of input into output. 

Production Function is an expression of the technological relationship between the physical inputs and outputs of a good.

The term “product” describes the volume of goods produced by a business or industry over a certain period.

The product concept can be seen from three different perspectives:

1. Total Product
2. Marginal Product
3. Average Product

1. Total Product (TP):

Total Product refers to the total quantity of goods produced by a firm during a given period of time with a given number of units. For example, if 5 labours produce 6 kg of wheat, then the total product is 30 kg. A company can increase TP in the short term by focusing primarily on the variable components. But over time, both fixed and variable elements can be increased to raise TP. Other names of Total Product are Total Physical Product, Total Return, or Total Output.

2. Average Product (AP):

Average Product refers to output per unit of a variable input. For example, if the total product is 30 kg of wheat produced by 5 labours(variable inputs), then the average product will be 30/5, i.e., 6 kg. AP is calculated by dividing TP by units of the variable factor.

Formula:

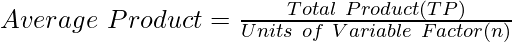
TP in terms of AP will be: 

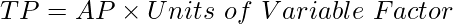
3. Marginal Product (MP):

Marginal Product refers to the addition to the total product when one more unit of a variable factor is employed. It calculates the extra output per additional unit of input while keeping all other inputs constant. Other names of Marginal Product are Marginal Physical Product (MPP) or Marginal Return.

Formula:

MP_n = TP_n – TP_n-1

Where, 

MP_n = Marginal product of n^th unit of the variable factor

TP_n = Total product of n units of the variable factor

TP_n-1 = Total product of (n-1) units of the variable factor

n = Number of units of the variable factor 

One more way to calculate MP

MP is the change in TP when one additional unit of variable factor is used. However, when the change in variable factor exceeds one unit, MP can be calculated as:

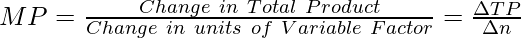
TP is the summation of MP:

Total Product can also be calculated as the sum of marginal product.

It means, 

TP = MP₁ + MP₂ + MP₃ +…………………..MP_n

or, 

TP= ΣMP

Relationship between TP and MP

Let’s take an example to understand the relationship between TP and MP.

Fixed Factor (Land) (in acres)	Variable Factor (Labour) (in units)	TP (units)	MP (units)
1	0	0	–
1	1	5	5
1	2	13	8
1	3	27	14
1	4	36	9
1	5	40	4
1	6	40	0
1	7	35	-5

Observation:

1. As long as the Total Product (TP) increases at an increasing rate; i.e., till point P, MP also increases.

2. When TP increases at a diminishing rate, MP also decreases. In this case, it starts happening when 4 units of labour are employed and continues till 6 units of the variable factor.

3. When TP reaches its maximum point; i.e., point M, MP becomes zero; i.e., point N.

4. Ultimately, when TP starts decreasing, MP becomes negative; i.e., from the 7^th unit.

In simple terms, the Relationship between TP and MP can be summarised as:

• MP increases when TP increases at an increasing rate
• MP starts declining when TP increases at a diminishing rate
• MP is zero when TP is maximum
• MP is negative when TP decreases

Relationship between AP and MP

Let’s take an example to understand the relationship between TP and MP.

Fixed Factor (Land) (in acres)	Variable Factor (Labour) (in units)	TP (units)	AP (units)	MP (units)
1	0	0	–	–
1	1	5	5	5
1	2	13	6.5	8
1	3	27	9	14
1	4	36	9	9
1	5	40	8	4
1	6	40	6.67	0
1	7	35	5	-5

Observation:

1. As long as MP is more than AP, AP rises. In this case, AP rises up to the 3^rd unit of the variable factor.

2. When MP is equal to AP, AP is at its maximum; i.e., at the 4^th unit of the variable factor.

3. When MP is less than AP, AP falls; i.e., from the 5^th unit of the variable factor.

4. Ultimately, both AP and MP fall but MP becomes negative and AP remains positive. Also, MP falls at a faster rate as compared to the fall in AP.

In simple terms, the Relationship between AP and MP can be summarised as:

• AP increases when MP>AP
• AP is constant and at its maximum point when MP = AP
• AP falls when MP<AP
• MP becomes negative, and AP remains positive