Relation in mathematics is defined as the well-defined relationship between two sets. The relation connects the value of the first set with the value of the second set. We represent relation in mathematics using the ordered pair. If we are given two sets Set X and Set Y then the relation between them is represented using the ordered pair (x, y) such that, x ϵ X and y ϵ Y.
Relations are used in mathematics, statistics, and data sciences. It is an integral part of RDBMS (Relational Database Management Systems) that is used in searching, storing, and sorting large data.
In this article, we will learn about, Relation in Mathematics, Example of Relation, Types of Relation, and others in detail.
What is Relation in Mathematics?
Relation in Mathematics is defined as the relationship between two sets. If we are given two sets set A and set B and set A has a relation with set B then each value of set A is related to a value of set B through some unique relation. Here, set A is called the domain of the relation, and set B is called the range of the relation.
For example if we are given two sets, Set A = {1, 2, 3, 4} and Set B = {1, 4, 9, 16} then the ordered pair {(1, 1), (2, 4), (3, 9), (4, 16)} represents the relation defined as, R, A: → B {(x, y): y = x2: y ϵ B, x ϵ A}.
Relation Definition
Relation is defined as the relation between two different sets of information. Suppose we are given two sets containing two different values then a relation defined such that it connects the value of the first set with the value of the second set is called the relation.
Suppose we are given a set A that contains the name of girls of a class and another set B that contains the height of girls then a relation connects set A with set B. In mathematical terms, we can say that,
“A set of ordered pairs is a relation”
Relations Examples
Example of relation in mathematics includes,
Suppose there are two sets X = {4, 36, 49, 50} and Y = {1, -2, -6, -7, 7, 6, 2}. A relation R states that
“(x, y) is in the relation R if x is a square of y” can be represented using ordered pairs,
- R = {(4, -2), (4, 2), (36, -6), (36, 6), (49, -7), (49, 7)}
Also, the image added below shows two sets A and B, and the relation between them,
Set A = {x, y, z}
Set B = {1, 2, 3}

Representation of Relations
In mathematics or in set theory we can represent the relation using different techniques and the two important ways to represent the set are,
- Set Builder Notation
- Roaster Notation
Let’s study them in detail in the article below,
Set Builder Notation
if are relation between two sets is represented using the logical formula then this type of representation is called the set builder notation.
For example, if we are given two sets set X = {2, 4, 6} and set Y = {4, 8, 12}. Then after observing clearly, we can see that each element of set Y is twice each element of set X the relation between them is,
- R {(a, b): b is twice of a, a ∈ X, b ∈ Y}
Roaster Form
Roaster form is another way of representing a relation. In roaster form, we use ordered pairs to represent the relation.
For example, if we are given two sets set X = {2, 4, 6} and set Y = {4, 8, 12}. Then the relation between set X and set Y is represented using the relation R such that,
- R = {(2, 4), (4, 8), (6, 12)}
Sets and Relations
Sets are the values that are arranged collectively. And relations are relationship that connects the values of two sets. So sets and relations are connected to each other. For example, if we are given two sets
- Set A = {-2, -1, 0, 1, 2}
- Set B = {2, 3, 4, 5, 6}
Then the relation that connects the two sets, set A and set B,
R = {(-2, 2), (-1, 3), (0, 4), (1, 5), (2, 6)}
Types of Relation
Various types of relations defined in mathematics are,
Now let’s learn about them in detail.
Empty Relation
A relation R on a set A is called Empty if the set A is an empty set, i.e. any relation where no element of set A is not related to the element of set B then it is called an empty relation. For example, A = {1, 2, 3} and B = {5, 6, 7} where, R = {(x, y) where x + y = 22}, then it is an empty relation.
Reflexive Relation
A relation R on a set A is called reflexive if (a, a) ∈ R holds for every element a∈ A . i.e. if set A = {a, b} then R = {(a, a), (b, b)} is reflexive relation.
For example, A = {2, 3} then the reflexive relation R on A is,
Symmetric Relation
A relation R on a set A is called symmetric if (b, a) ∈ R holds when (a, b) ∈ R i.e. The relation R = {(a, b), (b, a)} is a reflexive relation on (a, b)
For example, A = {2, 3} then symmetric relation R on A is,
Transitive Relation
A relation R on a set A is called transitive if (a, b) ∈ R and (b, c) ∈ R then (a, c) ∈ R for all a,b,c ∈ A i.e.
For example, set A = {1, 2, 3} then transitive relation R on A is,
- R = {(1, 2), (2, 3), (1, 3)}
Equivalence Relation
A relation is an Equivalence Relation if it is reflexive, symmetric, and transitive. i.e. relation R = {(1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2), (1, 3), (3, 1)} on set A = {1, 2, 3} is equivalence relation as it is reflexive, symmetric, and transitive.
Universal Relation
Universal relation is a relation in which all elements of set are mapped to other element of set then it is called universal relation. For example, A = {4, 8, 12} and B = {1, 2, 3} then universal relation is, R = {(x, y) where x > y}
Identity Relation
Identity relation is a relation defined such all elements in a set are related to itself. It is defined as, I = {(x, x) : for all x ∈ X}.
For example P = {1, 2, 3} then Identity Relation(I) = {(1, 1), (2, 2), (3, 3)}
Inverse Relation
A relation is called the inverse of any relation if elements of one set is inverse pair of another set. Inverse of a relation R is denoted as R-1. i.e., R-1 = {(y, x): (x, y) ∈ R}.
Graphing Relations
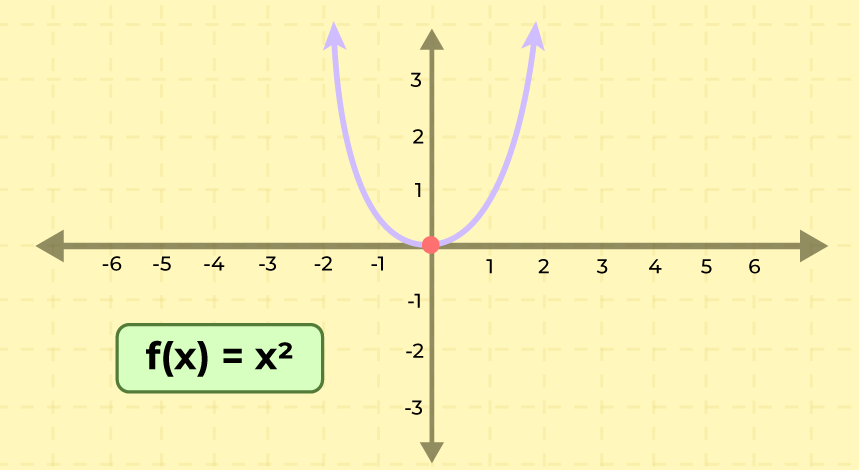
Relations can be easily represents on the graphs and representing them on graphs is an easy way of explaining them. The ordered pair in a relation represents a coordinate that can be plot on cartesian coordinate system. We can easily graph the relation by following the steps added below,
- Substitue x with random numerical values in the relation.
- Find the corresponding y value of the respective x value.
- Write the ordered pair such that, {(x, y)}
- Plot these points and join them to find the required curve.
The graph of the relation y = x2 is added below,
Read More,
Examples on Relations
Example 1: Find the inverse relation of R = {(1, 3), (2, 4), (3, 5)}
Solution:
Inverse relation is defined as R-1 = {(y, x): (x, y) ∈ R}
Given,
R = {(1, 3), (2, 4), (3, 5)}
Inverse relation of R is R-1 then,
- R-1 = {(3, 1), (4, 2), (5, 3)}
Example 2: Find the inverse relation of R = {(a, x), (b, y), (c, z)}
Solution:
Inverse relation is defined as R-1 = {(y, x): (x, y) ∈ R}
Given,
R = {(a, x), (b, y), (c, z)}
Inverse relation of R is R-1 then,
- R-1 = {(x, a), (y, b), (z, c)}
Practice Questions on Relations
Q1. Check wether the relation R = {(a, b), (b, c), (c, a), (a, a)} is Equivalence relation on set A = {a, b, c}
Q2. Check wether the relation R = {(1, 1), (1, 3), (1, 1), (2, 2)} is Equivalence relation on set A = {1, 2, 3}
Q3. Find the inverse of the relation R = {(1, 1), (2, 4), (3, 9)}
Q4. Find the inverse of the relation R = {(2, 6), (3, 7), (5, 9)}
Relations in Mathematics – FAQs
1. What is Relations in Math?
Relation in maths is a relationship between two sets that represents how the value of the first set is connected to the value of the second set.
2. What are the Types of Relation?
Relations between two sets are of various types and some of them are added below,
- Empty Relation
- Reflexive Relation
- Symmetric Relation
- Transitive Relation
- Equivalence Relation
- Universal Relation
- Identity Relation
- Inverse Relation
3. What is Relations Class 11?
Relation is introduced to students in class 11 in set theory and a relation R in mathematics is defined as the subset of the cartesian product of X × Y, where X and Y are two non-empty sets.
4. What are Properties of Relations?
Various properties of the relation are,
- Reflexive Property
- Symmetric Property
- Transitive Property
All these properties are explained in the article above.
5. What is a Null Relation?
An empty relation in mathematics also called the null relation is a relation where no element of the first set is mapped with the element of the second set.
6. Is a Relation a Function?
A relation may or may not be a function. A function is a unique relation in which each element of set A is uniquely related to the element of set B which is not the case in Relation. So we can say that each function is a relation but not every relation is a function.
7. Which Relation is Not a Function?
A relation on two sets set A and set B is not a function if one element of set A is linked with more than one value of set B then it is a relation but not a function example, R {(-1, 1), (1, 1)} is a relation but not a function.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...