Regular languages and finite automata

Question 1

Given the language L = {ab, aa, baa}, which of the following strings are in L*?

• abaabaaabaa

• aaaabaaaa

• baaaaabaaaab

•  baaaaabaa

Question 2

Consider the languages L1 = [Tex]\\phi [/Tex]and L2 = {a}. Which one of the following represents L1 L2^* U L1^*

• {[Tex]\epsilon [/Tex]}

• [Tex]\phi [/Tex]

• a^*

• {[Tex]\epsilon [/Tex],a}

Question 3

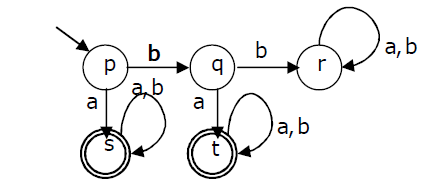
Consider the DFA given. 

[caption width="800"]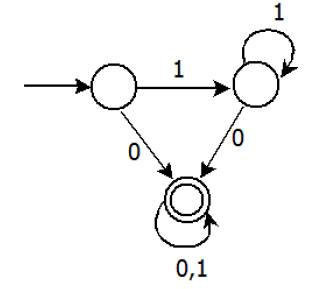 [/caption]

 Which of the following are FALSE?

• Complement of L(A) is context-free.

• L(A) = L((11*0+0)(0 + 1)*0*1*).

• For the language accepted by A, A is the minimal DFA.

• A accepts all strings over {0, 1} of length at least 2.

Question 4

Consider the set of strings on {0,1} in which, every substring of 3 symbols has at most two zeros. For example, 001110 and 011001 are in the language, but 100010 is not. All strings of length less than 3 are also in the language. A partially completed DFA that accepts this language is shown below. 

[caption width="800"] [/caption]

 The missing arcs in the DFA are 

• [caption width="800"] [/caption]
• [caption width="800"] [/caption]
• [caption width="800"] [/caption]
• [caption width="800"] [/caption]

Question 5

Definition of a language L with alphabet {a} is given as following.

             L={|ank|k>0, and n is a positive integer constant}

What is the minimum number of states needed in DFA to recognize L?

• k+1

• n+1

• 2⁽ⁿ⁺¹⁾

• 2[Tex](k+1)[/Tex]

Question 6

A deterministic finite automation (DFA)D with alphabet {a,b} is given below Which of the following finite state machines is a valid minimal DFA which accepts the same language as D?

• A
• B
• C
• D

Question 7

Let w be any string of length n is {0,1}*. Let L be the set of all substrings of w. What is the minimum number of states in a non-deterministic finite automaton that accepts L?

• n-1

• n

• n+1

• 2n-1

Question 8

Which one of the following languages over the alphabet {0,1} is described by the regular expression: (0+1)*0(0+1)*0(0+1)* ?

• The set of all strings containing the substring 00.
• The set of all strings containing at most two 0’s.
• The set of all strings containing at least two 0’s.
• The set of all strings that begin and end with either 0 or 1.

Question 9

Which one of the following is FALSE?

• There is unique minimal DFA for every regular language

• Every NFA can be converted to an equivalent PDA.

• Complement of every context-free language is recursive.

• Every nondeterministic PDA can be converted to an equivalent deterministic PDA.

Question 10

Given the following state table of an FSM with two states A and B, one input and one output:

Present State A	Present State B	Input	Next State A	Next State B	Output
0	0	0	0	0	1
0	1	0	1	0	0
1	0	0	0	1	0
1	1	0	1	0	0
0	0	1	0	1	0
0	1	1	0	0	1
1	0	1	0	1	1
1	1	1	0	0	1

If the initial state is A=0, B=0, what is the minimum length of an input string which will take the machine to the state A=0, B=1 with Output = 1?

• 3

• 4

• 5

• 6