Regression Analysis and the Best Fitting Line using C++
Last Updated :
28 Jul, 2022
This article discusses the basics of linear regression and its implementation in the C++ programming language. Regression analysis is the common analysis method that is used by data scientists for the prediction of values corresponding to some input data.
The simple regression analysis method is linear regression. Linear regression is a statistical method for modeling relationships between a dependent variable with a given set of independent variables. We are going to implement the same in C++.
The input data set generally comes in a .csv (comma-separated values) file which we will copy from that file and put in a .txt file as an input file for our C++ program. To take input from a file create an input.txt named file in the same directory as the program file and put the data inside that file such that the first line has the value of N i.e the number of entries in that dataset.
Implementation :
C++
#include <iostream>
#include <stdio.h>
#include <vector>
using namespace std;
class regression {
vector<float> x;
vector<float> y;
float coeff;
float constTerm;
float sum_xy;
float sum_x;
float sum_y;
float sum_x_square;
float sum_y_square;
public:
regression()
{
coeff = 0;
constTerm = 0;
sum_y = 0;
sum_y_square = 0;
sum_x_square = 0;
sum_x = 0;
sum_xy = 0;
}
void calculateCoefficient()
{
float N = x.size();
float numerator
= (N * sum_xy - sum_x * sum_y);
float denominator
= (N * sum_x_square - sum_x * sum_x);
coeff = numerator / denominator;
}
void calculateConstantTerm()
{
float N = x.size();
float numerator
= (sum_y * sum_x_square - sum_x * sum_xy);
float denominator
= (N * sum_x_square - sum_x * sum_x);
constTerm = numerator / denominator;
}
int sizeOfData()
{
return x.size();
}
float coefficient()
{
if (coeff == 0)
calculateCoefficient();
return coeff;
}
float constant()
{
if (constTerm == 0)
calculateConstantTerm();
return constTerm;
}
void PrintBestFittingLine()
{
if (coeff == 0 && constTerm == 0) {
calculateCoefficient();
calculateConstantTerm();
}
cout << "The best fitting line is y = "
<< coeff << "x + " << constTerm << endl;
}
void takeInput(int n)
{
for (int i = 0; i < n; i++) {
char comma;
float xi;
float yi;
cin >> xi >> comma >> yi;
sum_xy += xi * yi;
sum_x += xi;
sum_y += yi;
sum_x_square += xi * xi;
sum_y_square += yi * yi;
x.push_back(xi);
y.push_back(yi);
}
}
showData()
{
for (int i = 0; i < 62; i++) {
printf("_");
}
printf("\n\n");
printf("|%15s%5s %15s%5s%20s\n",
"X", "", "Y", "", "|");
for (int i = 0; i < x.size(); i++) {
printf("|%20f %20f%20s\n",
x[i], y[i], "|");
}
for (int i = 0; i < 62; i++) {
printf("_");
}
printf("\n");
}
float predict(float x)
{
return coeff * x + constTerm;
}
float errorSquare()
{
float ans = 0;
for (int i = 0;
i < x.size(); i++) {
ans += ((predict(x[i]) - y[i])
* (predict(x[i]) - y[i]));
}
return ans;
}
float errorIn(float num)
{
for (int i = 0;
i < x.size(); i++) {
if (num == x[i]) {
return (y[i] - predict(x[i]));
}
}
return 0;
}
};
int main()
{
freopen("input.txt", "r",
stdin);
regression reg;
int n;
cin >> n;
reg.takeInput(n);
reg.PrintBestFittingLine();
cout << "Predicted value at 2060 = "
<< reg.predict(2060) << endl;
cout << "The errorSquared = "
<< reg.errorSquare() << endl;
cout << "Error in 2050 = "
<< reg.errorIn(2050) << endl;
}
|
Content of input.txt file is:
84
1714, 2.4
1664, 2.52
1760, 2.54
1685, 2.74
1693, 2.83
1670, 2.91
1764, 3
1764, 3
1792, 3.01
1850, 3.01
1735, 3.02
1775, 3.07
1735, 3.08
1712, 3.08
1773, 3.12
1872, 3.17
1755, 3.17
1674, 3.17
1842, 3.17
1786, 3.19
1761, 3.19
1722, 3.19
1663, 3.2
1687, 3.21
1974, 3.24
1826, 3.28
1787, 3.28
1821, 3.28
2020, 3.28
1794, 3.28
1769, 3.28
1934, 3.28
1775, 3.29
1855, 3.29
1880, 3.29
1849, 3.31
1808, 3.32
1954, 3.34
1777, 3.37
1831, 3.37
1865, 3.37
1850, 3.38
1966, 3.38
1702, 3.39
1990, 3.39
1925, 3.4
1824, 3.4
1956, 3.4
1857, 3.41
1979, 3.41
1802, 3.41
1855, 3.42
1907, 3.42
1634, 3.42
1879, 3.44
1887, 3.47
1730, 3.47
1953, 3.47
1781, 3.47
1891, 3.48
1964, 3.49
1808, 3.49
1893, 3.5
2041, 3.51
1893, 3.51
1832, 3.52
1850, 3.52
1934, 3.54
1861, 3.58
1931, 3.58
1933, 3.59
1778, 3.59
1975, 3.6
1934, 3.6
2021, 3.61
2015, 3.62
1997, 3.64
2020, 3.65
1843, 3.71
1936, 3.71
1810, 3.71
1987, 3.73
1962, 3.76
2050, 3.81
Output:
The best fitting line is y = 0.00165565x + 0.27511
Predicted value at 2060 = 3.68575
The errorSquared = 3.63727
Error in 2050 = 0.140807
Explanation:
1. If all the data items into a graph are plotted then we will get several points in the graph, now the best fitting line is a line that is closest to every point on the graph.
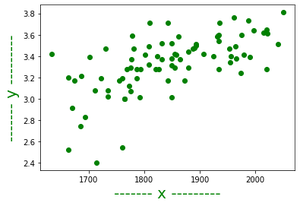
Graphical representation of data
2. Next task is to find the best fitting line. As any straight line can be represented in the form of y = ax + b, where a is the coefficient or slope of the line and b is the constant term.
3. So to find the best fitting line calculate the values of a and b. There is a straightforward formula for calculating the values of a and b which looks like the below ones-
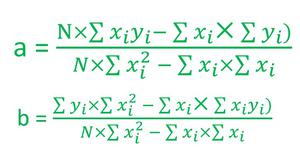
Formulae for a and b
4. After the value of a and b is calculated one can represent the line on the graph as:
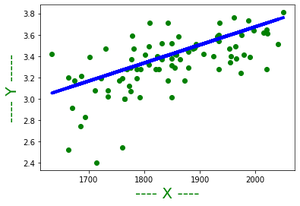
The best-fitting line
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...