Refraction is an important term used in the Ray Optics branch of Physics. Refraction of light is defined as the change in direction or the bending of a wave passing from one medium to another due to the change in speed of the wave. Some natural phenomena occurring in nature where refraction of light takes place are the twinkling of stars, the formation of mirages and Rainbows, Optical illusions, and many more. The major cause of refraction to occur is the change in the speed of waves in different mediums, which is different due to the difference between the densities of the mediums. e.g. the speed of light in a vacuum is maximum. Snell’s Law provides a quantitative description of the amount of bending of a wave, that depends on the refractive index of the two mediums. Let’s learn more about refraction like the Laws of Refractions, Causes of Refraction, Types of Refraction, Examples, and Applications of Refractions in the article below.
What is Refraction of Light?
The bending of a light wave when it passes from one medium to another due to the change in the speed of the light traveling the two different media is called the Refraction of light.
This phenomenon also occurs with sound, water, and other waves. Because of this bending of waves that are responsible for the refraction of light, we have lenses, magnifying glasses, prisms, and rainbows. Due to this phenomenon, our eyes would not be able to focus, without the refraction of light.
As shown in the above figure, light travels from Medium 1 to Medium 2. Please note that these mediums can be different materials or substances with different densities. So when an incident ray from medium 1 travels to another medium 2, the refracted ray bends either towards the normal or away from the normal (depending upon the densities of the mediums).
Here are the definitions of important terms used to study Refraction:
- Normal – The point of the surface at which an optical phenomenon occurs is called the normal. In simple words, it is termed the point of incidence. It is shown by a dotted line drawn perpendicular to the surface of the refracting material, in a ray diagram.
- Incident Ray – The light rays that strike the refracting surface, at the separation of two media are called the Incident Ray.
- Refracted Ray – The light rays that bend after passing into another medium are called the Refracted Ray.
- Angle of Incidence – This is the angle between the incident ray and the normal. It is represented by ∠i and it is also called an Incident angle.
- Angle of Refraction – This is the angle between refracted ray and the normal. It is represented by ∠r and it is also called a Refracted angle.
Laws of Refraction of Light
The refraction of light traveling through different mediums follows some laws. There are two laws of refraction as stated below which at the sight of refraction, the light follows, and we see the refracted image of the object.
- The reflected, incident, and the normal at the point of incidence all will tend to lie in the same plane.
- Secondly, the ratio of the sine of the angle of the incidence and refraction is constant which is termed Snell’s law.
sin i / sin r = Constant (n)
where i is the angle of incidence, r is the angle of refraction, the constant value depends on the refractive indexes of the two mediums.
What is the Refractive Index?
The Refractive index also called the index of refraction enables us to know how fast light travels through the material medium.
Refractive Index is a dimensionless quantity. For a given material or medium, the refractive index is considered the ratio between the speed of light in a vacuum (c) to the speed of light in the medium (v) on which it goes. The Refractive index for a medium is represented by small n, and it is given by the following formula:
n = c / v
where
- c is the speed of the light in a vacuum, and
- v is the speed of light in the medium.
The given velocities of light in different media can give the refractive index by the following also where the first medium is not vacuum:
n21 = v1 / v2
where n21 is the refractive index of 2 with respect to 1.
Based on the given refractive index of the material or medium, the light ray either changes its direction or bends at the junction which separates the two given media. If the light ray travels from a certain medium to another of a slightly higher refractive index, it bends towards the normal in that case when traveling from rarer to a denser medium, or else it bends away from the normal when traveling from denser to rarer medium.
Snell’s Law
Snell’s law provides the degree or extent of refraction that occurs through a relationship between the incident angle, refracted angles, and the refractive indices of a given pair of media.
According to Snell’s law, the ratio of the sine of the incident angle to the sine of the refracted angle is a constant, for any light of a given color or for any given pair of media. The constant value is called the refractive index of the second medium with respect to the first.
Snell’s Law is given by the relation,

or

where,
- i and r are the angle of incidence and refraction,
- n is the refractive index and n1 and n2 are the refractive indices of medium 1 and 2, and
- v1 and v2 are the speed of light in medium 1 and 2 respectively.
Causes of Refraction of Light
As it is known that when light travels in different mediums its speed varies. e.g. light passes through the air than in a glass. Hence, it can be said that, due to the change in the speed of light in different mediums that the light rays are refracted.
To understand the causes of refraction of light in much depth let’s understand What are rarer and denser mediums? and Types of Refractions as:
What are Rarer and Denser mediums?
- Rarer medium (or Optically Rarer medium) is a medium in which the speed of light is more. For example, Air is optically rarer medium as compared to glass and water.
- Denser medium (or Optically Denser medium) is a medium in which the speed of light is less. For example, Glass is optically denser medium as compared to air.
Types of Refraction
The refraction of light occurs in different ways depending on the medium through which the light travels.
- Refraction from denser to rarer medium – When light rays pass through rarer to a denser medium, the light rays bend towards the normal. Due to this the angle of refraction is smaller than the angle of incidence. e.g. In the case when light rays pass from air to water or from air to glass, it bends towards normal. It is because of the reason that the speed of light rays reduces while passing from air to glass or water.
- Refraction from rarer to denser medium – When light rays pass from denser to rarer medium, the light rays bend away from the normal. Due to this the angle of refraction becomes more than the angle of incidence. e.g. In case when light rays pass from water to air or glass to air, light rays bend away from the normal. The speed of light rays becomes greater while passing from glass or water to air.
Characteristics of Refraction
Some of the important characteristics of Refraction are:
- The frequency of light does not change when it travels from one medium to another, but the velocity and wavelength of light changes.
- A ray of light bends when it travels from one optical medium to another with a variable refractive index. For a specific pair of media, the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant.
- The relationship between a medium’s refractive index and the speed of light in that medium is as follows:

where,
- i and r are the angle of incidence and refraction,
- n is the refractive index and n1 and n2 are the refractive indices of medium 1 and 2, and
- v1 and v2 are the speed of light in medium 1 and 2 respectively.
Effects of Refraction of Light
When anything interrupts the light waves, it causes refraction of the light. Light also moves mostly in the form of waves, much like most other materials.
As shown below, the pencil seems deformed in the water because light cannot travel through the water as rapidly as it can through the air. The pencil has a tiny magnification effect due to the light refraction, which makes the angle appear larger than it actually is and makes the pencil appear crooked.
Examples of Refraction of Light
- The stars twinkle in the night sky due to the refraction of their light.
- Looming and Mirage formation, both occur due to the optical illusions caused by the refraction of light.
- The formation of rainbows in the sky and VIBGYOR, when white light passes through the prism are also major examples of refraction.
- A swimming pool always seems or looks much shallower than it really is because of the light that comes from the bottom of the pool bends at the surfaces due to the refraction of light.
Applications of Refraction of Light
Refraction has many wide and common applications in optics and also in technology. A few of them are given below:
- A lens uses the refraction phenomenon to form an image of an object or body for various purposes, such as magnification.
- Spectacles that are worn by people with defective vision use the principle of refraction.
- Refraction is used in peepholes of the house doors for safety, in cameras, inside movie projectors, and also in telescopes.
Solved Examples on Refraction of Light
Example 1: What is the constant value if the angle of incidence is 22° and the angle of refraction is given to be 15°?
Solution:
As we know,
sin i / sin r = constant
Given sin i = sin 22° and sin r = sin 22°
Putting the values of angles from log table we get
sin 22° / sin 15° = 1.44
Hence, the value of constant or refractive index is 1.44.
Example 2: What is the constant value if the angle of incidence is 30° and the angle of refraction is given to be 46°?
Solution:
Since, the
sin i / sin r = constant
Given sin i= sin 30° and sin r= sin 46°
Putting the values of angles from log table we get
sin 30° / sin 46° = 1.44
Hence, the constant is 1.44.
Example 3: What is the value of the sine of the angle of incidence if the angle of refraction is given to be sin 35°? Given the value of refractive index 1.33.
Solution:
As we know,
{sin i}/{sin r} =constant
Given constant= 1.33 and sin r = sin 35° = 0.57
Putting the values of angles from log table we get
sin i / sin 35° = 1.33
sin i = 1.33 × 0.57
= 0.75
Example 4: Calculate the speed of light in diamond with respect to air. Take the absolute refractive index of glass from the table.
Solution:
As we know we can calculate refractive index by the following formula,
n = c/v
where refractive index of diamond n= 2.42, c = 3 × 108 m/s
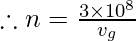
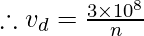
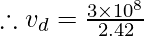
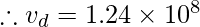
Hence, the velocity or speed of light in glass is vd = 1.24 × 108 m/s
FAQs based on Refraction of light
Question 1: Define the term Refraction.
Answer:
The change that occurs in the direction of a wave when light passes from one medium to the other is known as refraction of light.
Question 2: When is the refraction of light not possible?
Answer:
When the light is incident perpendicular to the boundary or surface, refraction of light is not possible.
Question 3: What is the difference between reflection and refraction in light?
Answer:
The bouncing back of light when it strikes a smooth surface is called Reflection. While the bending of a light ray when it travels from one medium to other is called refraction of light.
Question 4: Give an example of the Refraction of light.
Answer:
There are many examples of refraction of light observed in our daily life like the Twinkling of stars. The Twinkling of stars is because of the atmospheric refraction occurs by the light from the star undergoing a gradual change in the medium.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...