When the medium changes, the velocity and wavelength vary, but the frequency remains constant. The velocity of light remains constant in a particular medium. Light seems to travel along a straight-line path in a transparent medium. But what happens when it travels from one transparent medium to another, the answer is refraction.
Consider the apparent displacement of a pencil partially immersed in water. The light that reaches you from the section of the pencil that is submerged appears to emanate from a different direction than the one that is above water. The pencil seems to be shifted at the interface as a result of this. From this, we can say that light does not travel in the same direction in all media, thus when travelling obliquely from one medium to another, the direction of propagation of light in the second medium changes. This phenomenon is called the Refraction of light.
When a monochromatic ray of light travels from one transparent medium into another transparent medium, its direction changes (except for normal incidence).
Laws of Refraction
- First law of Refraction: The incident ray and the refracted ray are on the opposite sides of the normal at the point of incidence and all three lie in the same plane.
- Second law of Refraction: For a given pair of media, the ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant. (The constant is called the refractive index of the second medium with respect to the first medium). It is written as,
1μ2 = sin i / sin r = Constant
This is called Snell`s law.
When a ray of light travels from medium 1 into medium 2, then Snell`s law is written as,
1μ2 = 1n2 sin i / sin r
where,
i is the angle of incidence in 1st medium,
r is the angle of refraction in 2nd medium, and
1n2 is the relative refractive index.
Refraction at the Curved Surfaces

Refraction at Curved Surface
Consider the APB of a spherical surface that divides medium-1 and medium-2. Let μ1 represent the refractive index of medium-1 and μ2 represent the refractive index of medium-2 (μ2 > μ1) where C is the centre of curvature, R is the radius of curvature and i is the angle of incidence.
Now, Consider an object ‘O’ in medium – 1. Incident ray OP travels unaffected through medium-2 along with PI. Consider a second ray OD that is incident on the surface and makes an angle of incidence ‘i’ at point D. After refraction, it bends towards the normal CD and intersects the axis at the point I. As a result, point I is a true representation of point object O. Therefore, OP represents the Distance of the object from the surface, PI represents the Distance of the image from the surface, and PC represents Radius of curvature (since C is center of curvature).
Looking at the above figure and according to the new Cartesian sign convention, we can say that, object distance OP is -ve and image distance (PI) and radius of curvature (PC) are +ve.
Therefore,
- Object distance = OP = -u
- Image distance = PI = +v
- Radius of curvature = PC = +R
Let α, β, δ be the angles made by OD, ID and CD with the principal axis. From Snell`s Law, we can write,
μ2 / μ1 = sin i / sin r …….(1)
Now if we consider the point D to be very close to point P, then all the angles, i, r, α, β, δ will also be small, So in terms of radians,
sin i = i and sin r = r
μ1 i = μ2 r …….(2)
From figure,
∠i = ∠α + ∠δ (By Exterior angle theorem)
Similarly,
∠δ = ∠r + ∠β
or,
∠r = ∠δ – ∠β
Substituting both the values in equation (2) we get,
μ1 (α + β) = μ2 (δ – β)
μ1 α + μ2 β = ( μ2 – μ1 ) δ …….(3)
As angles are small, we can express them in radians as,
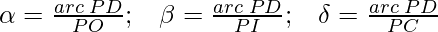
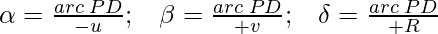
Substituting these values in equation (3) as,
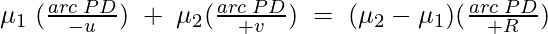
μ2 / v – μ1 / u =( μ2 – μ1 )/ R
The above expression gives the relation between u, v, μ1, μ2 and R for refraction at the curved surface.
This expression is obtained for the real images but is equally applicable for virtual images and for any pair of refracting media. While using the above expression the quantities, v, u, R are to be used with their appropriate sign (as per the new sign Cartesian system).
Applications of Refraction at the Curved Surfaces
- A lens is used for refraction to generate a picture, similar to magnification.
- peepholes in the door, magnifying glasses used in the lab.
- Another use of refraction is VIBGYOR, which is how white light is divided into the spectrum of colours as it travels through a glass prism.
- To rectify refractive defects in human eyes, refractive concave and convex glasses are used.
- Mirage, or the twinkling of stars, is a prominent example of atmospheric refraction.
Sample Problems
Problem 1: A ray of light is incident on the surface of the water at an angle of incidence of 70°. The ray is deviated from 25° towards normal when it enters the water. Calculate the refractive index of water.
Solution:
Given that,
i = 70°
δ = 25°
Since, it is known that,
δ = i – r
r = i – δ
= 45°
Also,
μ = sin i / sin r
= sin 70° / sin 45°
= 0.9397 / 0.7071
= 1.33
The refractive index of water is 1.33.
Problem 2: A spherical surface of radius of curvature 5 cm separates water and glass. An object is placed on the principal axis in water at 50 cm from the surface. Find the position of the image if the surface is,
(Refractive index of water is 4/3 and that of glass is 1.5).
Solution:
Given that,
u = object distance = -50cm
μ1 = refractive index of water = 4/3
μ2 = refractive index of glass = 1.5
Due to refraction at curved surface,
μ2 / v – μ1 / u =( μ2 – μ1 )/ R
μ2 / v =( μ2 – μ1 )/ R + μ1 / u
- For concave surface R = -5cm
1.5 / v = [1.5 – (4 / 3) / (-5)] + [(4 / 3) / -50]
v = -25 cm
A virtual image is formed at 25 cm from the pole and on the same side of object.
- For convex surface R = +5cm
1.5 / v = [1.5 – (4 / 3) / (+5)] + [(4 / 3) / -50]
v = 225 cm
A real image is formed at 225 cm from the pole and on the other side of surface.
Problem 3: A convex surface separates two media of refractive indices 1.3 and 1.5. if the radius of curvature is 20cm and an object is placed 260 cm from the refracting surface, calculate the distance of the image from the surface.
Solution:
Given that,
μ1 = 1.3
μ2 = 1.5
R = +20cm
u = -260cm (object distance)
Therefore,
μ2 / v – μ1 / u =( μ2 – μ1 )/ R
1.5 / v – 1.3 / (-260) = (1.5 – 1.3) / 20
1.5 / v = 0.2 / 20 – 1.3 / 260
This implies,
v = 300 cm
The image distance from surface is 300 cm.
Problem 4: A point object in air is situated on the principal axis of a convex glass surface 15 cm from its pole, the refractive index of glass 1.5, and the radius of curvature of the spherical surface is 30 cm. Find the position of the image and state its nature.
Solution:
Given that,
u = -15cm
μ1 = 1
μ2 =1.5
R = 30cm
Therefore,
μ2 / v – μ1 / u =( μ2 – μ1 )/ R
or
μ2 / v =( μ2 – μ1 )/ R + μ1 / u
So,
1.5 / v = ( 1.5 – 1 ) / 30 + (1 / -15)
1.5 / v = -(1 / 20)
This implies,
v = -20 × 1.5
= -30 cm
The image is located 30 cm from the pole, on the same side as the object. And the nature of image is Virtual.
Problem 5: A point object is placed at 8cm from the centre of a glass sphere of radius 2 cm and refractive index 1.6. Draw the ray diagram and find the image when viewed from a diametrically opposite position.
Solution:
Given that,
Object distance = 8 cm
Radius = 2 cm
Refractive index = 1.6
Ray diagram:

A paraxial ray OD suffers two refractions, at the two sides of the glass sphere. For refraction at the side 1, the refracted ray is DE. Had the medium (glass) been continuously beyond P1 ,the ray DE would have formed a real image let`s say at I1 . Thus, in this case
u = P1O = -6 cm
mage distance v` = P1I1
R = P1C = 2cm
μ1 = 1
μ2 = 1.6
We have,
μ2 / v – μ1 / u =( μ2 – μ1 )/ R
μ2 / v =( μ2 – μ1 )/ R + μ1 / u
1.6 / v’ = (1.6 – 1) / 2 + 1 / (-6)
= 0.6 / 2 – 1 / 6
= 0.8 / 6
v’ = 1.6 × 6 / 0.8
= 12 cm
For the refraction at the second side, the incidence ray DE is in the glass, the refracted ray is in the air and I1 acts as the virtual object with object distance
P2I1 = P1I1 – P1P2 = 12cm – 4cm = 8cm
Thus, in this case,
u = P2I1 = 8
image distance = v = P2I
R = P2C = -2cm
μ1 = 1.6
μ2 = 1
μ2 / v = (μ2 – μ1) / R + μ2 / u
1 / v = (1 – 1.6) / (-2) + (1.6 / 8)
= 0.3 + 0.2 = 0.5
v = 1 / 0.5
= 2 cm
The final image (real) is formed in air on the side of the observer at a distance of 4cm from the centre of the sphere.
Share your thoughts in the comments
Please Login to comment...