Reduced Row Echelon Form (rref) Matrix in MATLAB
Last Updated :
14 May, 2021
Reduced Row Echelon Form of a matrix is used to find the rank of a matrix and further allows to solve a system of linear equations. A matrix is in Row Echelon form if
- All rows consisting of only zeroes are at the bottom.
- The first nonzero element of a nonzero row is always strictly to the right of the first nonzero element of the row above it.
Example :
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccccc} 1 & a_0 & a_1 & a_2 & a_3 \\ 0 & 0 & 2 & a_4 & a_5 \\ 0 & 0 & 0 & 1 & a_6\\ 0 & 0 & 0 & 0 & 0 \end{array} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-18dbb03b0b8d6ba22db9611e96b6cd2d_l3.png)
A matrix can have several row echelon forms. A matrix is in Reduced Row Echelon Form if
- It is in row echelon form.
- The first nonzero element in each nonzero row is a 1.
- Each column containing a nonzero as 1 has zeros in all its other entries.
Example:
![Rendered by QuickLaTeX.com {\displaystyle \left[{\begin{array}{ccccc}1&0&a_{1}&0&b_{1}\\0&1&a_{2}&0&b_{2}\\0&0&0&1&b_{3}\end{array}}\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fcb5f352abe0990a1cf37e2048cf23ea_l3.png)
Where a1,a2,b1,b2,b3 are nonzero elements.
A matrix has a unique Reduced row echelon form. Matlab allows users to find Reduced Row Echelon Form using rref() method. Different syntax of rref() are:
- R = rref(A)
- [R,p] = rref(A)
Let us discuss the above syntaxes in detail:
rref(A)
It returns the Reduced Row Echelon Form of the matrix A using the Gauss-Jordan method.
Matlab
A = magic(4);
disp("Matrix");
disp(A);
RA = rref(A);
disp("rref :");
disp(RA);
|
Output :

rref(A)
- It returns Reduced Row Echelon Form R and a vector of pivots p
- p is a vector of row numbers that has a nonzero element in its Reduced Row Echelon Form.
- The rank of matrix A is length(p).
- R(1:length(p),1:length(p)) (First length(p) rows and length(p) columns in R) is an identity matrix.
Matlab
A = magic(5);
disp("Matrix");
disp(A);
[RA,p] = rref(A);
disp("rref :");
disp(RA);
disp("Pivot vector");
disp(p);
|
Output :

Finding solutions to a system of linear equations using Reduced Row Echelon Form:
The System of linear equations is
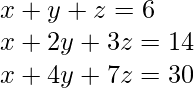
Coefficient matrix A is
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccccc} 1 & 1 & 1 \\ 1 & 2 & 3\\ 1 & 4 & 7 \end{array} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5e87e92ebc048c1f360583d7e24a20bf_l3.png)
Constant matrix B is
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccccc} 6 \\ 14\\ 30 \end{array} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-862022e7b44e4a353cea6e0fe61bde76_l3.png)
Then Augmented matrix [AB] is
![Rendered by QuickLaTeX.com \left[ \begin{array}{ccccc} 1 & 1 & 1 & 6\\ 1 & 2 & 3 & 14\\ 1 & 4 & 7 & 30 \end{array} \right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bf654edc5901b34733544255ae41db2e_l3.png)
Matlab
A = [1 1 1;
1 2 3;
1 4 7];
b = [6 ;14; 30];
M = [A b];
disp("Augmented matrix");
disp(M)
R = rref(M);
disp("rref");
disp(R)
|
Output :

Then the reduced equations are 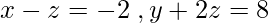
It has infinite solutions, one can be 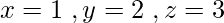 .
.
Share your thoughts in the comments
Please Login to comment...