Reduce given three Numbers by decrementing in Pairs

Given three integers A, B, and C. In one operation, choose any two of the three integers, subject to the condition that both of them should be greater than 0, and reduce them by 1. The task is to find the maximum number of operations that can be performed until at least two of them become 0.

Examples:

Input: A = 1, B = 3, C = 1 
Output: 2 
Explanation:
Operation 1: Choose A and B, reduce both by 1. Current values: A = 0, B = 2, C = 1 
Operation 2: Choose B and C, reduce both by 1. Current Values: A = 0, B = 1, C = 0 
No more operations are possible as any pair chosen will have at least one 0 in it.
Input: A = 8, B = 1, C = 4 
Output: 5 

Approach: The idea is to arrange the given numbers in decreasing order to find the maximum number of operations on the basis of the following condition: 
Case 1: When A ? (B + C)

• Choose pairs A and B for B times. As a result, after B operations the current status will be A = (A – B) and B = 0.
• As A ? (B + C) implies (A – B) ? C. So the pair A and C can be chosen for C operations, and the current status will be A = (A – B – C), B = 0, and C = 0.
• Total operations performed = (B + C)

Case 2: When A < (B + C)

• Try to make A, B, C equal after performing some operations.
• First, make A and B equal. For this choose A and C for performing (A – B) operations. Let the updated values be named A₁, B₁ , and C₁. The values A₁, B₁, and C₁ will be: 

A₁ = A – (A – B) 
B₁ = B 
C₁ = C – (A – B)

• The number of operations performed = (A – B).
• A₁ and B₁ are equal. So, choose the pair A₁ and B₁ for (A₁ – C₁) operations.
• Let A₂, B₂, and C₂ be the updated values of A, B, and C after the above operation. The values of A₂, B_2, and C₂ Will be the same and that will be: 

A₂ = A₁ – (A₁ – C₁) = C₁ = (C – A + B)
B₂ = C – A + B
C₂ = C – A + B

• Let the total number of operations performed as of now be Z. So the value of Z will be: 

Z = (A – B) + (A₁ – C₁) = (A – B) + (B – C + A – B)= 2A – B – C

• As A2 = B2 = C2, then there arises two cases: 
  
  • A2, B2, C2 are even: For every set of 3 operations on the pairs (A2, B2), (B2, C2), and (C2, A2) the count of the A2, B2, and C2 decreases by 2. 
    Let A2 = B2 = C2 = 4. Let the operations that can be performed be X. So, X = (4 + 4 + 4) / 2 = 6. Thus, the value of X can be generalized as: 

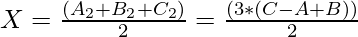
• A2, B2, C2 are odd: For every set of 3 operations on the pairs (A2, B2), (B2, C2), and (C2, A2) the count of the A2, B2, and C2 decreases by 2, finally, the values A2, B2, and C2 reach 1, 1 and 1 respectively. Here one additional operation can be performed. 
  Let A2 = B2 = C2 = 5. After performing 6 operations, A2 = B2 = C2 = 1. Here one more operation can be performed. Therefore, total operations that can be performed are 7 (6+1). Let the operations that can be performed be Y. So, Y = floor((5 + 5 + 5) / 2) = 7. Thus, the value of Y can be generalized as:

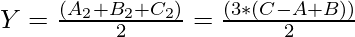
• Since from the above steps X = Y, therefore a total number of possible causes can be given by:

Total number of possible cases = (Z + X) = (Z + Y) = (A + B + C) / 2.  

Below is the implementation of the above approach: 

C++

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to find the minimum number
// operations
int solution(int A, int B, int C)
{
    int arr[3];

    // Insert the three numbers in array
    arr[0] = A, arr[1] = B, arr[2] = C;

    // Sort the array
    sort(arr, arr + 3);

    // Case 2
    if (arr[2] < arr[0] + arr[1])
        return ((arr[0] + arr[1]
                 + arr[2])
                / 2);
    // Case 1
    else
        return (arr[0] + arr[1]);
}

// Driver Code
int main()
{
    // Given A, B, C
    int A = 8, B = 1, C = 5;

    // Function Call
    cout << solution(A, B, C);
    return 0;
}

Java

// Java program for the above approach
import java.util.*;

class GFG{

// Function to find the minimum number
// operations
public static int solution(int A, int B, int C)
{
    int arr[] = new int[3];

    // Insert the three numbers in array
    arr[0] = A; arr[1] = B; arr[2] = C;

    // Sort the array
    Arrays.sort(arr);

    // Case 2
    if (arr[2] < arr[0] + arr[1])
        return ((arr[0] + arr[1] + arr[2]) / 2);

    // Case 1
    else
        return (arr[0] + arr[1]);
}

// Driver Code
public static void main(String[] args)
{

    // Given A, B, C
    int A = 8, B = 1, C = 5;

    // Function call
    System.out.println(solution(A, B, C));
}
}

// This code is contributed by jrishabh99

Python

#Python3 program for the above approach
#Function to find the minimum number
#operations
def solution(A, B, C):
    arr=[0] * 3

    #Insert the three numbers in array
    arr[0] = A
    arr[1] = B
    arr[2] = C

    #Sort the array
    arr = sorted(arr)

    #Case 2
    if (arr[2] < arr[0] + arr[1]):
        return ((arr[0] + arr[1] + arr[2]) // 2)

    #Case 1
    else:
        return (arr[0] + arr[1])

#Driver Code
if __name__ == '__main__':

    #Given A, B, C
    A = 8
    B = 1
    C = 5

    #Function Call
    print(solution(A, B, C))

# This code is contributed by Mohit Kumar 29

C#

// C# program for the above approach
using System;

class GFG{

// Function to find the minimum number
// operations
public static int solution(int A, int B, int C)
{
    int []arr = new int[3];

    // Insert the three numbers in array
    arr[0] = A; arr[1] = B; arr[2] = C;

    // Sort the array
    Array.Sort(arr);

    // Case 2
    if (arr[2] < arr[0] + arr[1])
        return ((arr[0] + arr[1] + arr[2]) / 2);

    // Case 1
    else
        return (arr[0] + arr[1]);
}

// Driver Code
public static void Main(String[] args)
{

    // Given A, B, C
    int A = 8, B = 1, C = 5;

    // Function call
    Console.WriteLine(solution(A, B, C));
}
}

// This code is contributed by Rajput-Ji

Javascript

<script>
// JavaScript program for the above approach

// Function to find the minimum number
// operations
function solution(A, B, C)
{
    let arr = Array.from({length: 3}, (_, i) => 0);

    // Insert the three numbers in array
    arr[0] = A; arr[1] = B; arr[2] = C;

    // Sort the array
    arr.sort();

    // Case 2
    if (arr[2] < arr[0] + arr[1])
        return ((arr[0] + arr[1] + arr[2]) / 2);

    // Case 1
    else
        return (arr[0] + arr[1]);
}

// Driver Code

    // Given A, B, C
    let A = 8, B = 1, C = 5;

    // Function call
    document.write(solution(A, B, C));

</script>

Output:

6

Time Complexity: O(1) 
Space Complexity: O(1)