Rectangle with minimum possible difference between the length and the width
Last Updated :
09 Jan, 2023
Given an integer area, the task is to find the length and breadth of a rectangle with the given area such that the difference between the length and the breadth is the minimum possible.
Examples:
Input: area = 99
Output: l = 11, b = 9
All possible rectangles (l, b) are (99, 1), (33, 3) and (11, 9)
And the one with the minimum |l – b| is (11, 9)
Input: area = 25
Output: l = 5, b = 5
Approach: The task is to find two integers l and b such that l * b = area and |l – b| are as minimal as possible. Factorization can be used to solve the problem, but doing just simple factorization from 1 to N will take a long time to get the required output for larger values of N.
To overcome this, just iterate up to. Considering  < l ? N, then for all values of l, b will always be <
< l ? N, then for all values of l, b will always be <  .
.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void find_rectangle(int area)
{
int l, b;
int M = sqrt(area), ans;
for (int i = M; i >= 1; i--) {
if (area % i == 0) {
l = (area / i);
b = i;
break;
}
}
cout << "l = " << l << ", b = "
<< b << endl;
}
int main()
{
int area = 99;
find_rectangle(area);
return 0;
}
|
Java
class GFG {
static void find_rectangle(int area)
{
int l = 0, b = 0;
int M = (int)Math.sqrt(area), ans;
for (int i = M; i >= 1; i--) {
if (area % i == 0) {
l = (area / i);
b = i;
break;
}
}
System.out.println("l = " + l + ", b = " + b);
}
public static void main(String[] args)
{
int area = 99;
find_rectangle(area);
}
}
|
Python3
import math as mt
def find_rectangle(area):
l, b = 0, 0
M = mt.ceil(mt.sqrt(area))
ans = 0
for i in range(M, 0, -1):
if (area % i == 0):
l = (area // i)
b = i
break
print("l =", l, ", b =", b)
area = 99
find_rectangle(area)
|
C#
using System;
class GFG {
static void find_rectangle(int area)
{
int l = 0, b = 0;
int M = (int)Math.Sqrt(area);
for (int i = M; i >= 1; i--) {
if (area % i == 0) {
l = (area / i);
b = i;
break;
}
}
Console.WriteLine("l = " + l + ", b = " + b);
}
public static void Main()
{
int area = 99;
find_rectangle(area);
}
}
|
PHP
<?php
function find_rectangle($area)
{
$M = floor(sqrt($area));
for ($i = $M; $i >= 1; $i--)
{
if ($area % $i == 0)
{
$l = floor($area / $i);
$b = $i ;
break;
}
}
echo "l = ", $l, ", b = ", $b, "\n";
}
$area = 99;
find_rectangle($area);
?>
|
Javascript
<script>
function find_rectangle(area)
{
let l = 0, b = 0;
let M = Math.floor(Math.sqrt(area)), ans;
for (let i = M; i >= 1; i--) {
if (area % i == 0) {
l = Math.floor(area / i);
b = i;
break;
}
}
document.write("l = " + l + ", b = " + b);
}
let area = 99;
find_rectangle(area);
</script>
|
Time Complexity: O(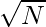 )
)
Auxiliary Space: O(1)
Below is a simple implementation.
CPP
#include <bits/stdc++.h>
using namespace std;
void find_rectangle(int area)
{
for (int i = ceil(sqrt(area)); i <= area; i++) {
if (area / i * i == area) {
printf("%d %d", i, area / i);
return;
}
}
}
int main()
{
int area = 99;
find_rectangle(area);
return 0;
}
|
Java
import java.io.*;
class GFG {
static void find_rectangle(int area)
{
for(int i = (int)Math.ceil(Math.sqrt(area)); i <= area; i++)
{
if(area / i * i == area)
{
System.out.println(i + " " + (int)(area / i));
return;
}
}
}
public static void main (String[] args)
{
int area = 99;
find_rectangle(area);
}
}
|
Python3
import math
def find_rectangle(area):
for i in range(int(math.ceil(math.sqrt(area))) , area + 1):
if((int(area / i) * i) == area):
print(i, int(area / i))
return
area = 99
find_rectangle(area)
|
C#
using System;
class GFG
{
static void find_rectangle(int area)
{
for(int i = (int)Math.Ceiling(Math.Sqrt(area)); i <= area; i++)
{
if(area / i * i == area)
{
Console.WriteLine(i + " " + (int)(area / i));
return;
}
}
}
static void Main()
{
int area = 99;
find_rectangle(area);
}
}
|
Javascript
<script>
function find_rectangle(are)
{
for(let i = Math.floor(Math.ceil(Math.sqrt(area))); i <= area; i++)
{
if(Math.floor(area / i) * i == area)
{
document.write(i + " " + Math.floor(area / i));
return;
}
}
}
let area = 99;
find_rectangle(area);
</script>
|
Time Complexity: O(log(area)), due to inbuild function sqrt()
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...