Reaching a point using clockwise or anticlockwise movements
Last Updated :
20 Feb, 2023
Given starting and ending position and a number N. Given that we are allowed to move in only four directions as shown in the image below. The directions of moves are U( ), R
), R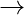 , D
, D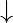 and L
and L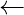 . We need to write a program to determine if starting from the given starting position we can reach the given end position in exactly N moves in moving about any direction(Clockwise or Anticlockwise).
. We need to write a program to determine if starting from the given starting position we can reach the given end position in exactly N moves in moving about any direction(Clockwise or Anticlockwise).

Examples :
Input: start = U , end = L , N = 3
Output: Clockwise
Explanation: Step 1: move clockwise to reach R
Step 2: move clockwise to reach D
Step 3: move clockwise to reach L
So we reach from U to L in 3 steps moving in
clockwise direction.
Input: start = R , end = L , N = 3
Output: Not possible
Explanation: It is not possible to start from
R and end at L in 3 steps moving about in any
direction.
Input: start = D , end = R , N = 7
Output: Clockwise
Explanation: Starting at D, we complete one
complete clockwise round in 4 steps to reach D
again, then it takes 3 step to reach R
The idea to solve this problem is to observe that we can complete one round in 4 steps by traveling in any direction (clockwise or anti-clockwise), so taking n%4 steps is equivalent to taking n steps from the starting point. Therefore n is reduced to n%4. Consider the values of ‘U’ as 0, ‘R’ as 1, ‘D’ as 2 and ‘L’ as 3. If the abs(value(a)-value(b)) is 2 and n is also 2, then we can move either in clockwise or anticlockwise direction to reach the end position from the start position. If moving k steps in clockwise direction take us to the end position from start position then we can say that the condition for clockwise move will be (value(a)+k)%4==value(b). Similarly, the condition for anticlockwise move will be (value(a)+k*3)%4==value(b) since taking k step from position a in clockwise direction is equivalent to taking (a + k*3)%4 steps in anticlockwise direction.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int value(char a)
{
if (a == 'U')
return 0;
if (a == 'R')
return 1;
if (a == 'D')
return 2;
if (a == 'L')
return 3;
}
void printMove(char a, char b, int n)
{
n = n % 4;
if (n == 2 and abs(value(a) -
value(b)) == 2)
cout << "Clockwise or Anticlockwise";
else if ((value(a) + n * 3) % 4 == value(b))
cout << "Anticlockwise";
else if ((value(a) + n) % 4 == value(b))
cout << "Clockwise";
else
cout << "Not Possible";
}
int main()
{
char a = 'D', b = 'R';
int n = 7;
printMove(a, b, n);
return 0;
}
|
Java
class GFG
{
static int value(char a)
{
if (a == 'U')
return 0;
if (a == 'R')
return 1;
if (a == 'D')
return 2;
if (a == 'L')
return 3;
return -1;
}
static void printMove(char a,
char b,
int n)
{
n = n % 4;
if (n == 2 && Math.abs(value(a) -
value(b)) == 2)
System.out.println("Clockwise " +
" or Anticlockwise");
else if ((value(a) + n * 3) %
4 == value(b))
System.out.println("Anticlockwise");
else if ((value(a) + n) % 4 == value(b))
System.out.println("Clockwise");
else
System.out.println("Not Possible");
}
public static void main(String args[])
{
char a = 'D', b = 'R';
int n = 7;
printMove(a, b, n);
}
}
|
Python3
def value(a):
if (a == 'U'):
return 0
if (a == 'R'):
return 1
if (a == 'D'):
return 2
if (a == 'L'):
return 3
def printMove(a, b, n):
n = n % 4;
if (n == 2 and
abs(value(a) - value(b)) == 2):
print ("Clockwise or Anticlockwise")
elif ((value(a) + n * 3) % 4 == value(b)):
print ("Anticlockwise")
elif ((value(a) + n) % 4 == value(b)):
print ("Clockwise")
else:
print ("Not Possible")
a = 'D'
b = 'R'
n = 7
printMove(a, b, n)
|
C#
using System;
class GFG
{
static int value(char a)
{
if (a == 'U')
return 0;
if (a == 'R')
return 1;
if (a == 'D')
return 2;
if (a == 'L')
return 3;
return -1;
}
static void printMove(char a,
char b,
int n)
{
n = n % 4;
if (n == 2 && Math.Abs(value(a) -
value(b)) == 2)
Console.Write("Clockwise " +
"or Anticlockwise");
else if ((value(a) + n * 3) %
4 == value(b))
Console.Write("Anticlockwise");
else if ((value(a) + n) %
4 == value(b))
Console.WriteLine("Clockwise");
else
Console.WriteLine("Not Possible");
}
public static void Main()
{
char a = 'D', b = 'R';
int n = 7;
printMove(a, b, n);
}
}
|
PHP
<?php
function value($a)
{
if ($a == 'U')
return 0;
if ($a == 'R')
return 1;
if ($a == 'D')
return 2;
if ($a == 'L')
return 3;
}
function printMove($a, $b,$n)
{
$n = $n % 4;
if ($n == 2 and abs(value($a) -
value($b)) == 2)
echo "Clockwise or Anticlockwise";
else if ((value($a) + $n * 3) %
4 == value($b))
echo "Anticlockwise";
else if ((value($a) + $n) %
4 == value($b))
echo "Clockwise";
else
echo "Not Possible";
}
$a = 'D'; $b = 'R';
$n = 7;
printMove($a, $b, $n);
?>
|
Javascript
<script>
function value(a)
{
if (a == 'U')
return 0;
if (a == 'R')
return 1;
if (a == 'D')
return 2;
if (a == 'L')
return 3;
return -1;
}
function printMove(a, b, n)
{
n = n % 4;
if (n == 2 && Math.abs(value(a) -
value(b)) == 2)
document.write("Clockwise " +
" or Anticlockwise");
else if ((value(a) + n * 3) %
4 == value(b))
document.write("Anticlockwise");
else if ((value(a) + n) % 4 == value(b))
document.write("Clockwise");
else
document.write("Not Possible");
}
let a = 'D', b = 'R';
let n = 7;
printMove(a, b, n);
</script>
|
Output :
Clockwise
Time Complexity: O(1), as we are not using any loop or recursion to traverse.
Auxiliary Space: O(1), as we are not using any extra space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...