Ratio of area of two nested polygons formed by connecting midpoints of sides of a regular N-sided polygon

Given an N-sided polygon, the task is to find the ratio of the area of the N^th to (N + 1)^th N-sided regular nested polygons generated by joining the midpoints of the sides of the original polygon.

Examples :

Input: N = 3
Output: 4.000000
Explanation:

Nested Triangle

Ratio of the length of the sides formed by joining the mid-points of the triangle with the length of the side of the original triangle is 0.5. Hence, R = (Area of N^th triangle) / (Area of (N + 1)^th triangle) = 4

Input: N = 4
Output: 2.000000

Approach: The problem can be solved based on the following observations:

• Consider an N-sided regular polygon as shown in the figure below.

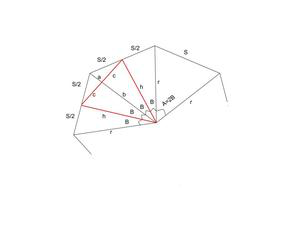
Representation Of Nested regular polygon of N sides.

• A = 2 * ? / N 
  B = ? / N 
  h = r * cos(B) 
  b = h * cos(B) 
  c = h((1 – cos(A)) / 2)^1/2
• Area of the Black Isosceles Triangle:

• Area of the Red Isosceles Triangle:

• r = s / (2 * [1 – cos(2B)])^1/2 and b = r * [cos(B)]²
• After combining the above equations:

• Final result obtained is as follows:

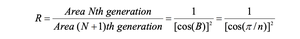
Below is the implementation of the above approach:

C++

// C++ code for the above approach
#include <bits/stdc++.h>
using namespace std;

// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
void AreaFactor(int n)
{
    // Stores the value of PI
    double pi = 3.14159265;

    // Calculating area the factor
    double areaf = 1 / (cos(pi / n)
                        * cos(pi / n));

    // Printing the ratio
    // precise upto 6 decimal places
    cout << fixed << setprecision(6)
         << areaf << endl;
}

// Driver Code
int main()
{
    int n = 4;
    AreaFactor(n);

    return 0;
}

Java

// Java program for the above approach
import java.io.*;

class GFG{

// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
static void AreaFactor(int n)
{

    // Stores the value of PI
    double pi = 3.14159265;

    // Calculating area the factor
    double areaf = 1 / (Math.cos(pi / n) *
                        Math.cos(pi / n));

    // Printing the ratio
    // precise upto 6 decimal places
    System.out.format("%.6f", areaf);
}

// Driver Code
public static void main(String[] args)
{
    int n = 4;

    AreaFactor(n);
}
}

// This code is contributed by code_hunt

Python3

# Python3 code for the above approach
import math

# Function to calculate the ratio of
# area of N-th and (N + 1)-th nested
# polygons formed by connecting midpoints
def AreaFactor(n):

    # Stores the value of PI
    pi = 3.14159265

    # Calculating area the factor
    areaf = 1 / (math.cos(pi / n) *
                 math.cos(pi / n))

    # Printing the ratio
    # precise upto 6 decimal places
    print('%.6f' % areaf)

# Driver Code
if __name__ == "__main__":

    n = 4
    AreaFactor(n)

# This code is contributed by ukasp

C#

// C# program for the above approach
using System;
using System.Collections.Generic;

class GFG {

// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
static void AreaFactor(int n)
{

    // Stores the value of PI
    double pi = 3.14159265;

    // Calculating area the factor
    double areaf = 1 / (Math.Cos(pi / n) *
                        Math.Cos(pi / n));

    // Printing the ratio
    // precise upto 6 decimal places
    Console.WriteLine(Math.Round(areaf));

}
    // Driver Code
    public static void Main(string[] args)
    {
        int n = 4;

        AreaFactor(n);
    }
}

// This code is contributed by susmitakundugoaldanga.

Javascript

<script>

// Javascript program implementation
// of the approach

// Function to calculate the ratio of
// area of N-th and (N + 1)-th nested
// polygons formed by connecting midpoints
function AreaFactor(n)
{
    // Stores the value of PI
    let pi = 3.14159265;

    // Calculating area the factor
    let areaf = (1 / (Math.cos(pi / n)
                        * Math.cos(pi / n)));

    // Printing the ratio
    // precise upto 6 decimal places
    document.write(areaf.toFixed(6));
}

// Driver Code

        let n = 4;
    AreaFactor(n);

// This code is contributed by splevel62.
</script>

Output:

2.000000

Time Complexity: O(1)
Auxiliary Space: O(1)