Ratio of area of one circle to the equilateral triangle when three equal circles are placed inside an equilateral triangle
Last Updated :
29 Oct, 2020
Given three equal circles that are placed inside an equilateral triangle such that every circle is tangential to the sides of the equilateral triangle and to other circles. The task is to find the ratio of the area of one circle to the area of the equilateral triangle.
Solution:
Below is the image of how circles are inscribed in a triangle:

Now since AB and BC are tangents to the circle with center P, PQ will be perpendicular to BC and PB will bisect angle ABC. Hence angle PBQ=30° since ABC is an equilateral triangle and angle ABC=60°.
Consider the triangle PBQ, tan30°= PQ/BQ = 1/√3
BQ = PQ*√3 = R*√3 (R is radius one circle). Similarly RC = R*√3
Now BC = BQ+QR+CR = R√3 + 2R + R√3 = 2R(√3 +1)
Therefore, the ratio of the area of the circle to the area of the triangle is given by:
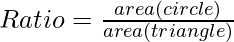
Since,
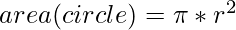 [Tex]area(triangle) = \frac{\sqrt{3}(2r(\sqrt{3}+1))^{2}}{4} [/Tex]
[Tex]area(triangle) = \frac{\sqrt{3}(2r(\sqrt{3}+1))^{2}}{4} [/Tex]
Therefore, the ratio is given by:
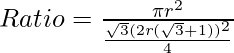 [Tex]Ratio = \frac{\pi}{\sqrt{3}(\sqrt{3}+1)^{2}} [/Tex]
[Tex]Ratio = \frac{\pi}{\sqrt{3}(\sqrt{3}+1)^{2}} [/Tex]
Share your thoughts in the comments
Please Login to comment...