Random Numbers Ecosystem in Julia – The Pseudo Side
Last Updated :
05 Dec, 2022
When we talk of randomness in general, it’s not something that shouldn’t possess repetition, it is something that outputs data that is unpredictable.
Random numbers are very essential when it comes to cryptography, MonteCarlo simulations, etc. For every time you log in to a service, make an online transaction, random numbers from the system are invoked in order to secure the process(encryption).
But our computers, specifically the CPU, are number-crunching beasts, that blindly follow the instructions that are fed to them. So they are virtually inapt to inherently pick any numbers. That’s where human intervention steps in.
Now there are two ways. The fast yet inefficient way and the slow yet near perfect way.
The former pertains to PRNGs(Pseudo Random Number Generators) and the latter to TRNGs(True Random Number Generators). Check out this link if you wish to try out some RNG algorithms.
Most operating systems(linux, windows etc.) have a built-in pool of randomness. from which random numbers for various uses are sampled. The entropy pool that consists of entropy(randomness) collected from various sources in the computer. Eg: The CPU/GPU thermals, timing of user keystrokes, mouse movement, cpu scheduling and other sensors that provide unpredictable input.
When random numbers are generated, the entropy of the pool is diminished since some of the information about the entropy pool is now given out. So it has to be replenished by a process called stirring.
Intel’s Ivy Bridge family of processors have an integrated feature viz. secure key, which refers to a dedicated random number generator inside them, composing a special instruction set called RDRAND that returns random numbers.
Coming to RNG’s in Julia. There is a good support for Pseudo random number generation in Julia.
Inherently Julia uses the Mersenne Twister library for random number generation. Besides MersenneTwister, Julia also provides the RandomDevice type, which wraps over the operating system provided entropy.
Random data generation
rand() Function
Syntax :
rand([rng=GLOBAL_RNG], [set..], [dimensions...])
Picks a random element or array of random elements from the set of values specified by set, where set can be :
- an indexable collection (for example 1:9 or (‘x’, “y”, :z)),
- an AbstractDict or AbstractSet object,
- a String
- a type(eg : struct)
Example:
Python3
rand(Int, 2)
rand((3, 5))
rand(Float64, (2, 3))
|
Output:

rand!() Function
RandomNumbers.jl is a library that provides extended support for random number generation.
Syntax:
rand!([rng=GLOBAL_RNG], Arr, [set=eltype(Arr)])
It populates the array Arr with random values. If set is specified, the values are picked randomly from set. It simply copies the random values generated from rand() to Arr but without allocating a new array.
Example:
Python3
using Random
rng = MersenneTwister(1234);
Arr = zeros(5)
rand !(rng, Arr)
|
Output :

bitrand() Function
Syntax :
bitrand([rng=GLOBAL_RNG], [dimensions])
It generates an Array (of type BitArray) containing random boolean values(0/1).
Example:
Python3
rng = MersenneTwister(1234);
bitrand(rng, 10)
|
Output :

randn() Function
Syntax:
randn([rng=GLOBAL_RNG], [T=Float64], [dimensions])
It generates a normally-distributed random number of type T with mean 0 and standard deviation 1. It will optionally generate an array of normally-distributed random numbers if the dimensions parameter is given.
Example:
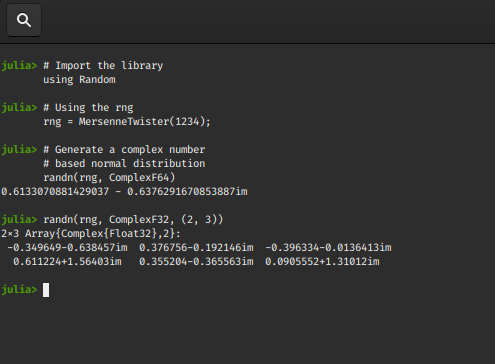
Python3
using Random
rng = MersenneTwister(1234);
randn(rng, ComplexF64)
randn(rng, ComplexF32, (2, 3))
|
Output:
randstring() Function
Syntax:
randstring([rng=GLOBAL_RNG], [characters], [length])
It creates a random string of size length, consisting of characters, which defaults to the set of upper- and lower-case letters and the digits 0-9. The optional rng argument specifies a random number generator.
Example:
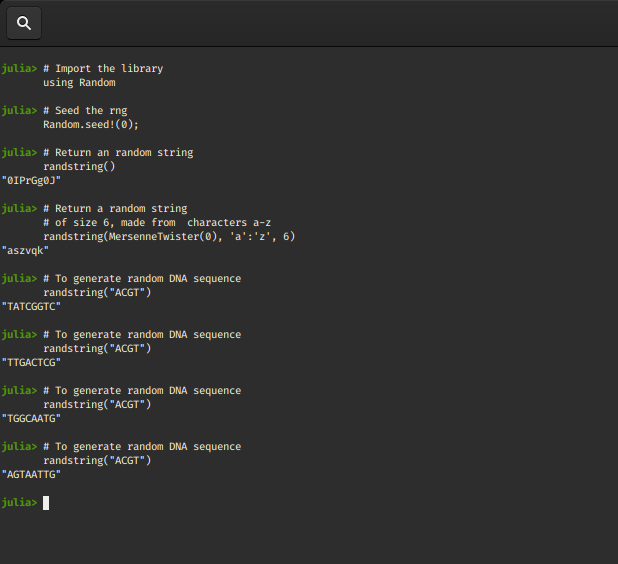
Python3
using Random
Random.seed !(0);
randstring()
randstring(MersenneTwister(0), 'a':'z', 6)
randstring("ACGT")
|
Output:
randperm() Function
Syntax:
randperm([rng=GLOBAL_RNG], n::Integer)
Construct a random permutation of length n.
Examples:
Python3
using Random
rng = MersenneTwister(1234);
randperm(rng, 4)
randperm !(rng, Vector{Int}(undef, 4))
|
Output:

RandomDevice() Function
Syntax :
RandomDevice()
Creates a RandomDevice RNG object that generates a stream of random numbers for which the entropy is obtained from the operating system.
Sampler() function
Syntax:
Sampler(rng, x, repetition)
It returns a sampler object that can be used to generate random values from rng for x.
When Sampler(rng, x, repetition), rand(rng, sp) is used to draw random values, repetition can be Val(1) or Val(Inf).
Example :
Python3
using Random
rng = RandomDevice()
s = Random.Sampler(rng, Val(1))
|
Output:

Generating values from a type
For a type T, it’s assumed that if rand(T) is defined, an object of type T will be produced. The default sampler for types is SamplerType.
Syntax:
rand(rng::AbstractRNG, ::Random.SamplerType{T})
Defines random generation for values of type T
This is particularly useful in cases like the classical example of a dice that gives a random number.
Python3
struct Dice
n::Int
end
Random.rand(rng::AbstractRNG, ::Random.SamplerType{Dice}) = Dice(rand(rng, 1:6))
rand(Dice)
rand(MersenneTwister(0), Dice)
|
Output:

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...