random header | Set 2 (Distributions)

Difficulty Level : Easy
Last Updated : 29 May, 2017

Distributions

I. Uniform :

uniform_int_distribution: It produces random integer values i, which are uniformly distributed on the closed interval [a,b], which is described by the following probability mass function:

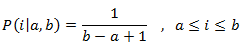
operator(): It generates the random number that are distributed according to the probability function.
min: It returns the greatest lower bound of the range of values returned by operator(), which is the distribution parameter ‘a’ for uniform_int_distribution.
max: It returns the least upper bound of the range of values returned by operator(), which is the distribution parameter ‘b’ for uniform_int_distribution.
reset: It resets the distribution, so that on the subsequent uses the result does not depends on the values already produced by it.

// C++ program to illustrate
// the use of operator()
// in uniform_int_distribution
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
      
    // Constructing a trivial random generator engine 
    unsigned s = 2;
      
    // The random number generator
    default_random_engine generator (s);
      
    uniform_int_distribution<int> distribution(1,10);
    cout << "Some random numbers between 1 and 10";
    for (int i = 0; i < 10; ++i)
        cout << distribution(generator) ;
      
    cout << endl;
      
    return 0;
}

Output:

Some random numbers between 1 and 10: 1 3 6 10 1 5 1 4 4 9

// C++ program to illustrate
// the use of reset
// in uniform_int_distribution
#include <iostream>
#include <random>
using namespace std;
  
//Driver program
int main()
{
          
    //the random number generator
    default_random_engine generator;
      
    // Initialising the uniform distribution
    uniform_int_distribution<int> distribution(1, 1000);
      
    // First random number is generated
    cout << distribution(generator) << endl;
      
    //Resets the distribution
    distribution.reset();
      
    // Second random number is 
    //generated independent of previous number
    cout << distribution(generator) << endl;
      
    return 0;
}

Output:

1
132

uniform_real_distribution: It is the random number distribution that produces floating-point values , which is described by the following probability density function:

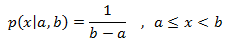
operator(): It returns a new random number that follows the distribution’s parameters.
min: It returns the greatest lower bound of the range of values returned by operator(), which is the distribution parameter ‘a’ for uniform_real_distribution.
max: It returns the least upper bound of the range of values returned by operator(), which is the distribution parameter ‘b’ for uniform_real_distribution.
reset: It resets the distribution, so that on the subsequent uses the result does not depend on values already produced by it.

// C++ program to illustrate
// the use of operator()
// in uniform_int_distribution
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
      
    // Constructing a trivial random generator engine 
    unsigned s = 2;
      
    // The random number generator
    default_random_engine generator (s);
      
    uniform_int_distribution<int> distribution(1,10);
    cout << "Random numbers between 1 and 10";
    for (int i = 0; i< 10; ++i)
        cout << distribution(generator) ;
      
    cout << endl;
      
    return 0;
}

Output:

some random numbers between 0.0 and 10.0: 
0.150031
9.77072
3.36669
7.06447
5.11455
8.43061
1.93792
7.78965
8.31532
5.14354

// C++ program to illustrate
// the use of reset
// in uniform_real_distribution
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
    default_random_engine generator;
    uniform_real_distribution<double> distribution(0.0,100.0);
      
    // It prints two independent values:
    // First random number is generated
    cout << distribution(generator) << endl;
      
    //Resets the distribution
    distribution.reset();
      
    // Second random number is 
    //generated independent of previous number
    cout << distribution(generator) << endl;
      
    return 0;
}

Output:

13.1538
45.865

II. Related to bernoulli trials:

bernoulli_distribution: It is the random number distribution that produces bool values according to a Bernoulli distribution, given by the following probability mass function:

operator(): It returns a new random number.
min: It returns the greatest lower bound of the range of values returned by operator(), which for bernoulli_distribution is false.
max: It returns the least upper bound of the range of values returned by operator(), which for bernoulli_distribution is true.

// C++ program to illustrate
// the bernoulli_distribution
#include <iostream>
#include <random>
using namespace std;
  
//Driver program
int main()
{
    const int temp=500;
      
    //The random number generator
    default_random_engine generator;
      
    //Initialising the bernoulli distribution
    bernoulli_distribution distribution(0.7);
      
    // count number of trues
    int count=0; 
      
    for (int i = 0; i < temp; ++i) 
    {
          
        // checking for true condition 
        if (distribution(generator)) 
        count++;
    }
      
    cout << "bernoulli_distribution (0.7) x 500:" << endl;
    cout << "true: " << count << endl;
    cout << "false: " << temp-count << endl;
      
    return 0;
}

Output:

bernoulli_distribution (0.7) x 500:
true:  360
false: 140

// C++ program to
// illustrate the use of reset
#include <iostream>
#include <random>
using namespace std;
  
//Driver program
int main()
{
    // Random number generator
    default_random_engine generator;
      
    // Initialising the bernoulli distribution
    bernoulli_distribution distribution;
      
    // print two independent values:
    cout << distribution(generator) << endl;
      
    // use of reset
    // Generates second output without
    // the effect of first output 
    distribution.reset();
    cout << distribution(generator) << endl;
  
return 0;
}

Output:

1
1

binomial_distribution: It is the random number distribution that produces integers according to a binomial discrete distribution, which is given by this probability mass function:

operator(): It generates a new random number.
max: It returns the least upper bound of the range given by operator(), which for binomial_distribution is the distribution parameter t.
min: It returns the greatest lower bound of the range given by member operator(), which for binomial_distribution is always zero.
reset: It resets the distribution, so that subsequent uses of the object do not depend on values already produced by it.

// C++ program to illustrate
// the use of binomial_distribution
#include <iostream>
#include <chrono>
#include <random>
using namespace std;
  
int main()
{
      
    // construct a trivial random 
    //generator engine from a time-based seed:
    unsigned seed = chrono::system_clock::now().time_since_epoch().count();
    default_random_engine generator (seed);
      
    // Initialising binomial distribution
    binomial_distribution<int> distribution (15, 0.4);
      
    cout << "some binomial results (t=15, p=0.4): ";
    for (int i = 0; i < 15; ++i)
    {
              
        // Use of operator()
        cout << distribution(generator) << " ";
    }
    cout << endl;
      
    return 0;
}

Output:

some binomial results (t=15, p=0.4): 7 6 7 8 4 6 7 6 9 3 5 6 4 6 7

// C++ program to illustrate
// the use of binomial_distribution
#include <iostream>
#include <chrono>
#include <random>
using namespace std;
  
int main()
{
      
    // construct a trivial random 
    //generator engine from a time-based seed:
    unsigned seed = chrono::system_clock::now().time_since_epoch().count();
    default_random_engine generator (seed);
      
    // Initialising binomial distribution
    binomial_distribution<int> distribution (15, 0.4);
      
    cout << "some binomial results (t=15, p=0.4): ";
    for (int i = 0; i < 15; ++i)
    {
              
        // Use of operator()
        cout << distribution(generator) << " ";
    }
    cout << endl;
      
    return 0;
}

Output:

57
52

geometric_distribution: It is a random number distribution that produces integers according to a geometric discrete distribution, given by the following probability mass function:

operator(): It returns a new random number that follows the distribution’s parameters.
max: It returns least upper bound of the range given by operator().
min: It returns the minimum value given by operator().
reset: It resets the distribution, so that subsequent uses of the object do not depend on values already produced by it.

// C++ program to illustrate
//the use of geometric_distribution 
#include <iostream>
#include <chrono>
#include <string>
#include <random>
using namespace std;
  
int main()
{
    // construct a trivial random
    // generator engine from a time-based seed:
    int seed = chrono::system_clock::now().time_since_epoch().count();
    default_random_engine generator (seed);
      
    // Initialises the geometric distribution
    geometric_distribution<int> distribution (1.0 / 5);
      
    cout << "Plus sign is 5 spaces away from the next :" << endl;
    for (int i = 0; i < 10 ; ++i) 
    {
        int number = distribution(generator);
        cout << string (number,' ') << "+";
    }
  
return 0;
}

Output:

each plus sign is 5 spaces away from the next :
            ++ + +   +  ++     +        ++

// C++ program to illustrate 
// the use of reset
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
      
    // Random number generator 
    default_random_engine generator;
      
    // Initialising the geometric distribution
    geometric_distribution<int> distribution(0.3);
      
    // Prints two independent values:
    // Generates the first value
    cout << distribution(generator) << endl;
      
    // Use of reset
    distribution.reset();
      
    // Generates second value
    cout << distribution(generator) << endl;
      
    return 0;
}

Output:

0
1

negative_binomial_distribution: It is a random number distribution that produces integers according to a negative binomial discrete distribution (also known as Pascal distribution), given by the following probability mass function:

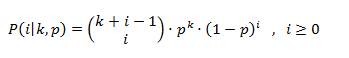
operator():It returns a new random number which follows the distribution’s parameters.
max:It returns least upper bound of the range given by operator().
min:It returns the minimum value given by operator(),which for negative_binomial_distribution is always zero.
reset: It resets the distribution, so that subsequent uses of the object do not depend on values already produced by it.

// C++ program to illustrate
// the use of operator() in
// negative_binomial_distribution 
#include <iostream>
#include <chrono>
#include <random>
using namespace std;
  
// Driver program
int main()
{
    // construct a trivial random 
    // generator engine from a time-based seed:
    unsigned seed = chrono::system_clock::now().time_since_epoch().count();
    default_random_engine generator (seed);
      
    // Initialising negative binomial distribution
    negative_binomial_distribution<int> distribution (6,0.7);
      
    cout << "Negative binomial results (t=6, p=0.7): ";
    for (int i = 0; i < 15; ++i)
        {
            // Use of operator
            cout << distribution(generator) << " ";
        }
      
    cout << endl;
      
    return 0;
}

Output:

Negative binomial results (t=6, p=0.7): 2 6 3 1 4 1 4 1 2 0 7 3 4 4 4

// C++ program to illustrate
// the use of reset in
// negative_binomial_distribution::
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
      
    // Random number generator 
    default_random_engine generator;
      
    // Initialising the negative binomial distribution
    negative_binomial_distribution<int> distribution(20, 0.5);
      
    // print two independent values:
    // Generates the first value
    cout << distribution(generator) << endl;
      
    // Use of reset
    distribution.reset();
      
    // Generates the second value
    cout << distribution(generator) << endl;
      
    return 0;
}

Output:

23
30

III.Piece wise distributions:

discrete_distribution: It is a random number distribution that produces integer values according to a discrete distribution.

operator(): It returns a new random number that follows the distribution’s parameters.
max: It returns the least upper bound of the range given by operator().
min: It returns the greatest lower bound of the range given by operator().
reset: It resets the distribution, so that subsequent uses of the object do not depend on values already produced by it.

// C++ program to illustrate the
// use of operator() in
// discrete_distribution
#include <iostream>
#include <random>
using namespace std;
  
int main()
{
      
    // number of experiments
    int n = 10000; 
      
    // maximum number of stars to distribute
    int m = 100; 
      
    // Random number generator
    default_random_engine generator;
      
    //Initialising discrete distribution
    discrete_distribution<int> distribution { 2, 2, 1, 1, 2, 2, 1, 1, 2, 2 };
      
    int p[10] = {};
      
    // use of operator()
    for (int i = 0; i < n; i++) 
    {
        int number = distribution(generator);
        p[number]++;
    }
      
    cout << "a discrete_distribution:" << endl;
    for (int i = 0; i < 10; ++i)
    {
        cout << i << ": " << string(p[i]*m/n,'*') << endl;
    }
      
    return 0;
}

Output:

a discrete_distribution:
0: ************
1: *************
2: *****
3: ******
4: ************
5: ************
6: ******
7: ******
8: ************
9: ************

// C++ program to illustrate
//the use of reset in
//discrete_distribution
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
      
    // Random number generator 
    default_random_engine generator;
      
    // Initialising the discrete distribution
    discrete_distribution<int> distribution {20,20,30,40};
      
    // print two independent values:
    // Generates the first value
    cout << distribution(generator) << endl;
      
    // Use of reset
    distribution.reset();
      
    // Generates the secong value
    cout << distribution(generator) << endl;
      
    return 0;
}

Output:

0
2

piecewise_constant_distribution: It is a random number distribution that produces floating-point values that are uniformly distributed over each of a sequence of contiguous subintervals, given by following probability density function:

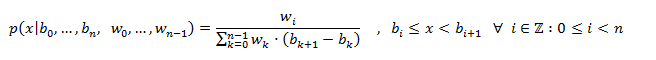
operator(): It returns a new random number that follows the distribution’s parameters.
max: It returns the least upper bound of the range given by operator().
min: It returns the greatest lower bound of the range given by operator().
reset: It resets the distribution, so that subsequent uses of the object do not depend on values already produced by it.

// C++ program to illustrate the
// use of reset in
// piecewise_constant_distribution
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
      
    // Random number generator
    default_random_engine generator;
      
    // Initialisind piecewise_constant_distribution
    piecewise_constant_distribution<double> distribution 
                ( 4, 0.0, 10.0, [](double x){return x;} );
      
    // print two independent values:
    // Generates the first value
    // Use of operator()
    cout << distribution(generator) << endl;
      
    // Use of reset
    distribution.reset();
      
    // Generates second value
    cout << distribution(generator) << endl;
      
    return 0;
}

Output:

3.4205
6.6692

piecewise_linear_distribution: It is a random number distribution that produces floating-point values that are distributed over a sequence of contiguous subintervals.

operator():It returns a new random number that follows the distribution’s parameters.
max: It returns the least upper bound of the range given by operator().
min: It returns the greatest lower bound of the range given by operator().
reset: It resets the distribution, so that subsequent uses of the object do not depend on values already produced by it.

// C++ program to illustrate the
// use of reset in
// piecewise_linear_distribution
#include <iostream>
#include <random>
using namespace std;
  
// Driver program
int main()
{
      
    // Random number generator
    default_random_engine generator;
      
    // Initialising piecewise_linear_distribution
    piecewise_linear_distribution<double>
        distribution ( 5, 0.0, 10.0, [](double x){return x+1.0;} );
      
    // print two independent values:
    // generates first value
    // use of operator()
    cout << distribution(generator) << endl;
      
    // Use of reset
    distribution.reset();
      
    // generates second value
    cout << distribution(generator) << endl;
      
    return 0;
}

Output:

2.48143
6.07656

This article is contributed by Shambhavi Singh. If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.

Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.

Want to learn from the best curated videos and practice problems, check out the C++ Foundation Course for Basic to Advanced C++ and C++ STL Course for foundation plus STL. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

My Personal Notes

Related Articles