Radius of the circle when the width and height of an arc is given

Given a circle in which the width and height of an arc are given. The task is to find the radius of the circle with the help of the width and height of the arc.
Examples:

Input: d = 4, h = 1 
Output: The radius of the circle is 2.5

Input: d = 14, h = 8
Output: The radius of the circle is 7.0625

Approach

• Let the radius of the circle be r
• Let the height and width of the arc be h & d
• Now, the diameter DC bisects the chord AB in two halves, each having length d/2
• Also the diameter is divided by the chord in two parts, the part inside arc h and the remaining 2r-h
• Now from intersecting chords theorem, 
  h*(2r-h) = (d/2)^2 
  or, 2rh – h^2 = d^2/4 
  so, r = d^2/8h + h/2
• So, radius of the circle 
  

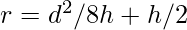
C++

// C++ program to find
// radius of the circle
// when the width and height
// of an arc is given

#include <bits/stdc++.h>
using namespace std;

// Function to find the radius
void rad(double d, double h)
{
    cout << "The radius of the circle is "
        << ((d * d) / (8 * h) + h / 2)
        << endl;
}

// Driver code
int main()
{
    double d = 4, h = 1;
    rad(d, h);
    return 0;
}

Java

// Java program to find
// radius of the circle
// when the width and height
// of an arc is given
class GFG
{

// Function to find the radius
static void rad(double d, double h)
{
    System.out.println( "The radius of the circle is "
        + ((d * d) / (8 * h) + h / 2));
}

// Driver code
public static void main(String[] args)
{
    double d = 4, h = 1;
    rad(d, h);
}
}

/* This code contributed by PrinciRaj1992 */

Python3

# Python3 program to find
# radius of the circle
# when the width and height
# of an arc is given

# Function to find the radius
def rad(d, h):
    print("The radius of the circle is",
        ((d * d) / (8 * h) + h / 2))

# Driver code
d = 4; h = 1;
rad(d, h);

# This code is contributed by 29AjayKumar

C#

// C# program to find
// radius of the circle
// when the width and height
// of an arc is given
using System;

class GFG
{

// Function to find the radius
static void rad(double d, double h)
{
    Console.WriteLine( "The radius of the circle is "
        + ((d * d) / (8 * h) + h / 2));
}

// Driver code
public static void Main()
{
    double d = 4, h = 1;
    rad(d, h);
}
}

// This code is contributed by AnkitRai01

PHP

<?php
// PHP program to find radius of
// the circle when the width and
// height of an arc is given

// Function to find the radius
function rad($d, $h)
{
    echo "The radius of the circle is ",
        (($d * $d) / (8 * $h) + $h / 2), "\n";
}

// Driver code
$d = 4;
$h = 1;
rad($d, $h);

// This code is contributed by ajit
?>

Javascript

<script>

// Javascript program to find
// radius of the circle
// when the width and height
// of an arc is given

// Function to find the radius
function rad(d, h)
{
    document.write("The radius of the circle is "
    +((d * d) / (8 * h) + h / 2));
}

// Driver code
    var d = 4, h = 1;
    rad(d, h);

</script>

Output:

The radius of the circle is 2.5

Time Complexity: O(1)

Auxiliary Space: O(1)