Qubit Representation
Last Updated :
23 Nov, 2020
Similar to a bit in classical computing, a
qubit is a basic building block of Quantum Computers. It represents the superposition of states 0 and 1. What we mean by superposition is that the given state is in a linear combination of state 0 and state 1.
It is a common misconception that qubit is in one state 0 or 1, we just don’t know until we measure it. However, qubit always exists in a state between 0 and 1 (inclusive), the act of measuring brings it to either of the states.
Matrix Representation :
A qubit is represented as a complex vector of size 2. Generally represented as :
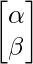
where
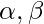
are amplitudes of states 0 and 1 respectively or we can say the probability to be in state 0 and 1 respectively. This vector is normalized i.e.
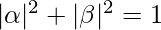
State 0 is represented as :
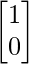
State 1 is represented as:

Quantum states |0> and |1> form orthogonal basis also called computational basis or canonical basis.
Dirac’s Notation :
It is a shorthand notation for a qubit. A vector is represented using a ket.
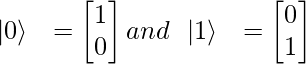
It also has a dual form written as:
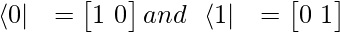
Hence, any arbitrary state can be represented as:
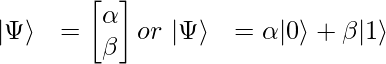
Some other symbols used are:
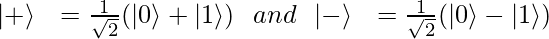
|+> and |-> are called Hadamard’s basis. These are also orthogonal to each other.
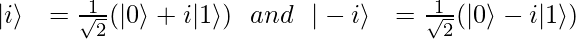 Bloch’s Representation :
Bloch’s Representation :
Bloch’s sphere is a geometric representation of quantum states where different points in the surface of the unit radius sphere represent various quantum states. A qubit can be represented in a 3D space as a vector of unit length connecting points in the surface of the Bloch’s sphere and it’s center.

Bloch’s Qubit Representation
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...