Quadratic Probing in Hashing

Hashing is an improvement technique over the Direct Access Table. The idea is to use a hash function that converts a given phone number or any other key to a smaller number and uses the small number as the index in a table called a hash table.

Hash Function:

A function that converts a given big number to a small practical integer value. The mapped integer value is used as an index in the hash table. In simple terms, a hash function maps a big number or string to a small integer that can be used as an index in the hash table. In this article, the collision technique, quadratic probing is discussed:

Quadratic Probing:

Quadratic probing is an open-addressing scheme where we look for the i²‘th slot in the i’th iteration if the given hash value x collides in the hash table.

How Quadratic Probing is done?

Let hash(x) be the slot index computed using the hash function.

If the slot hash(x) % S is full, then we try (hash(x) + 1*1) % S.
If (hash(x) + 1*1) % S is also full, then we try (hash(x) + 2*2) % S.
If (hash(x) + 2*2) % S is also full, then we try (hash(x) + 3*3) % S.
This process is repeated for all the values of i until an empty slot is found.

For example: Let us consider a simple hash function as “key mod 7” and sequence of keys as 50, 700, 76, 85, 92, 73, 101

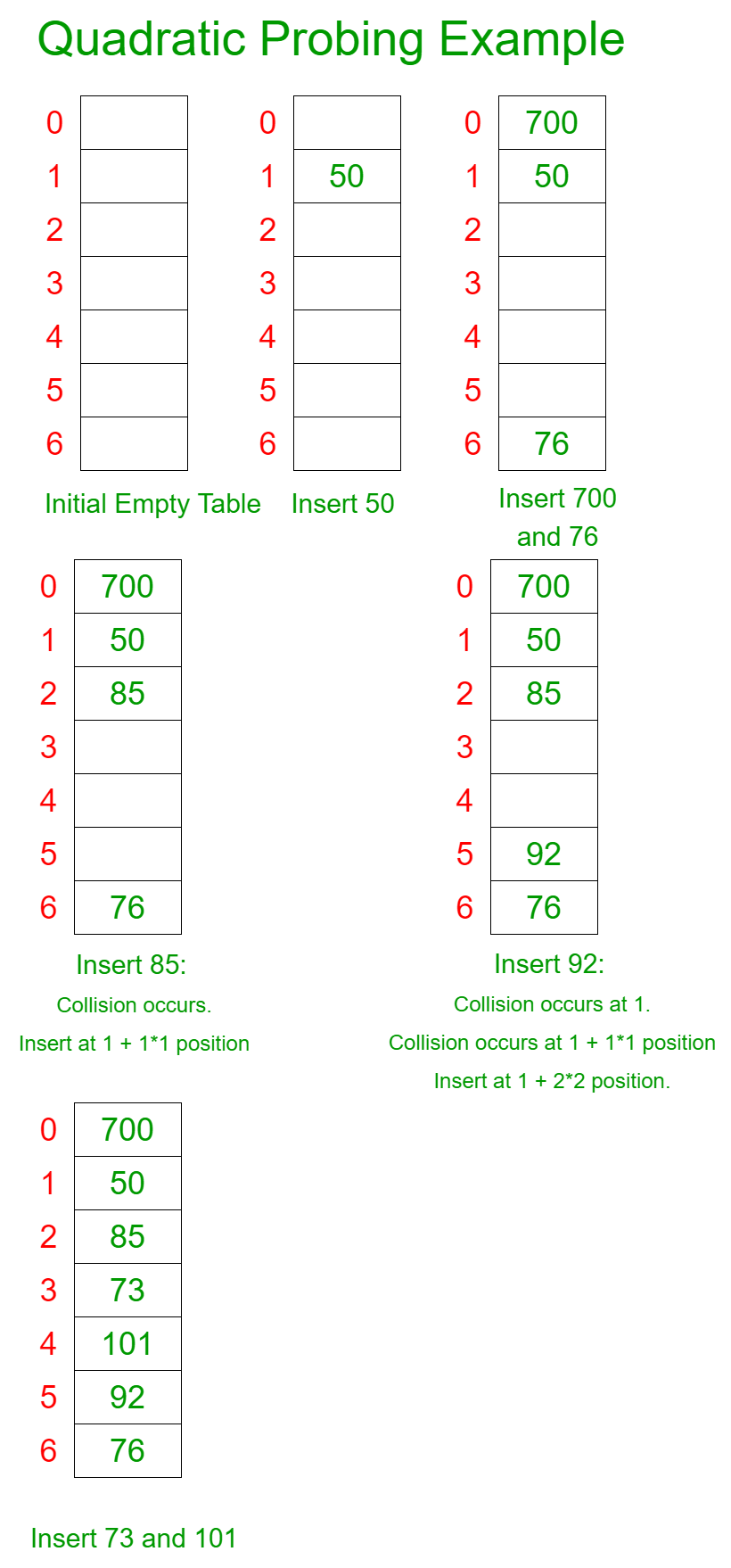
Below is the implementation of the above approach:

C++

// C++ implementation of
// the Quadratic Probing
#include <bits/stdc++.h>
using namespace std;
 
// Function to print an array
void printArray(int arr[], int n)
{
    // Iterating and printing the array
    for (int i = 0; i < n; i++) {
        cout << arr[i] << " ";
    }
}
 
// Function to implement the
// quadratic probing
void hashing(int table[], int tsize, int arr[], int N)
{
    // Iterating through the array
    for (int i = 0; i < N; i++) {
        // Computing the hash value
        int hv = arr[i] % tsize;
 
        // Insert in the table if there
        // is no collision
        if (table[hv] == -1)
            table[hv] = arr[i];
        else {
            // If there is a collision
            // iterating through all
            // possible quadratic values
            for (int j = 0; j < tsize; j++) {
                // Computing the new hash value
                int t = (hv + j * j) % tsize;
                if (table[t] == -1) {
                    // Break the loop after
                    // inserting the value
                    // in the table
                    table[t] = arr[i];
                    break;
                }
            }
        }
    }
    printArray(table, N);
}
 
// Driver code
int main()
{
    int arr[] = { 50, 700, 76, 85, 92, 73, 101 };
    int N = 7;
 
    // Size of the hash table
    int L = 7;
    int hash_table[7];
 
    // Initializing the hash table
    for (int i = 0; i < L; i++) {
        hash_table[i] = -1;
    }
 
    // Function call
    hashing(hash_table, L, arr, N);
    return 0;
}
 
// This code is contributed by gauravrajput1

Java

// Java implementation of the Quadratic Probing
 
class GFG {
 
    // Function to print an array
    static void printArray(int arr[])
    {
 
        // Iterating and printing the array
        for (int i = 0; i < arr.length; i++) {
            System.out.print(arr[i] + " ");
        }
    }
 
    // Function to implement the
    // quadratic probing
    static void hashing(int table[], int tsize, int arr[],
                        int N)
    {
 
        // Iterating through the array
        for (int i = 0; i < N; i++) {
 
            // Computing the hash value
            int hv = arr[i] % tsize;
 
            // Insert in the table if there
            // is no collision
            if (table[hv] == -1)
                table[hv] = arr[i];
            else {
 
                // If there is a collision
                // iterating through all
                // possible quadratic values
                for (int j = 0; j < tsize; j++) {
 
                    // Computing the new hash value
                    int t = (hv + j * j) % tsize;
                    if (table[t] == -1) {
 
                        // Break the loop after
                        // inserting the value
                        // in the table
                        table[t] = arr[i];
                        break;
                    }
                }
            }
        }
 
        printArray(table);
    }
 
    // Driver code
    public static void main(String args[])
    {
        int arr[] = { 50, 700, 76, 85, 92, 73, 101 };
        int N = 7;
 
        // Size of the hash table
        int L = 7;
        int hash_table[] = new int[L];
 
        // Initializing the hash table
        for (int i = 0; i < L; i++) {
            hash_table[i] = -1;
        }
 
        // Function call
        hashing(hash_table, L, arr, N);
    }
}

Python3

# Python3 implementation of
# the Quadratic Probing
 
# Function to print an array
 
 
def printArray(arr, n):
 
    # Iterating and printing the array
    for i in range(n):
        print(arr[i], end=" ")
 
# Function to implement the
# quadratic probing
 
 
def hashing(table, tsize, arr, N):
 
    # Iterating through the array
    for i in range(N):
 
        # Computing the hash value
        hv = arr[i] % tsize
 
        # Insert in the table if there
        # is no collision
        if (table[hv] == -1):
            table[hv] = arr[i]
 
        else:
 
            # If there is a collision
            # iterating through all
            # possible quadratic values
            for j in range(tsize):
 
                # Computing the new hash value
                t = (hv + j * j) % tsize
 
                if (table[t] == -1):
 
                    # Break the loop after
                    # inserting the value
                    # in the table
                    table[t] = arr[i]
                    break
 
    printArray(table, N)
 
 
# Driver code
if __name__ == "__main__":
    arr = [50, 700, 76,
           85, 92, 73, 101]
    N = 7
 
    # Size of the hash table
    L = 7
 
    hash_table = [0] * 7
 
    # Initializing the hash table
    for i in range(L):
        hash_table[i] = -1
 
    # Function call
    hashing(hash_table, L, arr, N)
 
# This code is contributed by code_hunt

C#

// C# implementation of the Quadratic Probing
using System;
 
class GFG {
 
    // Function to print an array
    static void printArray(int[] arr)
    {
 
        // Iterating and printing the array
        for (int i = 0; i < arr.Length; i++) {
            Console.Write(arr[i] + " ");
        }
    }
 
    // Function to implement the
    // quadratic probing
    static void hashing(int[] table, int tsize, int[] arr,
                        int N)
    {
 
        // Iterating through the array
        for (int i = 0; i < N; i++) {
 
            // Computing the hash value
            int hv = arr[i] % tsize;
 
            // Insert in the table if there
            // is no collision
            if (table[hv] == -1)
                table[hv] = arr[i];
            else {
 
                // If there is a collision
                // iterating through all
                // possible quadratic values
                for (int j = 0; j < tsize; j++) {
 
                    // Computing the new hash value
                    int t = (hv + j * j) % tsize;
                    if (table[t] == -1) {
 
                        // Break the loop after
                        // inserting the value
                        // in the table
                        table[t] = arr[i];
                        break;
                    }
                }
            }
        }
        printArray(table);
    }
 
    // Driver code
    public static void Main(String[] args)
    {
        int[] arr = { 50, 700, 76, 85, 92, 73, 101 };
        int N = 7;
 
        // Size of the hash table
        int L = 7;
        int[] hash_table = new int[L];
 
        // Initializing the hash table
        for (int i = 0; i < L; i++) {
            hash_table[i] = -1;
        }
 
        // Function call
        hashing(hash_table, L, arr, N);
    }
}
 
// This code is contributed by Rajput-Ji

Javascript

<script>
 
// Javascript implementation of the Quadratic Probing
 
    // Function to print an array
    function printArray(arr)
    {
   
        // Iterating and printing the array
        for (let i = 0; i < arr.length; i++) {
            document.write(arr[i] + " ");
        }
    }
   
    // Function to implement the
    // quadratic probing
    function hashing(table, tsize,
                        arr, N)
    {
   
        // Iterating through the array
        for (let i = 0; i < N; i++) {
   
            // Computing the hash value
            let hv = arr[i] % tsize;
   
            // Insert in the table if there
            // is no collision
            if (table[hv] == -1)
                table[hv] = arr[i];
            else {
   
                // If there is a collision
                // iterating through all
                // possible quadratic values
                for (let j = 0; j < tsize; j++) {
   
                    // Computing the new hash value
                    let t = (hv + j * j) % tsize;
                    if (table[t] == -1) {
   
                        // Break the loop after
                        // inserting the value
                        // in the table
                        table[t] = arr[i];
                        break;
                    }
                }
            }
        }
        printArray(table);
    }
      
    // Driver Code
    let arr = [ 50, 700, 76, 85,
                      92, 73, 101 ];
        let N = 7;
   
        // Size of the hash table
        let L = 7;
        let hash_table = [];
   
        // Initializing the hash table
        for (let i = 0; i < L; i++) {
            hash_table[i] = -1;
        }
   
        // Quadratic probing
        hashing(hash_table, L, arr, N);
 
// This code is contributed by splevel62.
</script>