median() function in Python statistics module
Last Updated :
27 Sep, 2021
Python is a very popular language when it comes to data analysis and statistics. Luckily, Python3 provide statistics module, which comes with very useful functions like mean(), median(), mode() etc.
median() function in the statistics module can be used to calculate median value from an unsorted data-list. The biggest advantage of using median() function is that the data-list does not need to be sorted before being sent as parameter to the median() function.
Median is the value that separates the higher half of a data sample or probability distribution from the lower half. For a dataset, it may be thought of as the middle value. The median is the measure of the central tendency of the properties of a data-set in statistics and probability theory. Median has a very big advantage over Mean, which is the median value is not skewed so much by extremely large or small values. The median value is either contained in the data-set of values provided or it doesn’t sway too much from the data provided.
For odd set of elements, the median value is the middle one.
For even set of elements, the median value is the mean of two middle elements.
Median can be represented by the following formula :
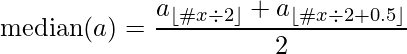
Syntax : median( [data-set] )
Parameters :
[data-set] : List or tuple or an iterable with a set of numeric values
Returns : Return the median (middle value) of the iterable containing the data
Exceptions : StatisticsError is raised when iterable passed is empty or when list is null.
Code #1 : Working
Python3
import statistics
data1 = [2, -2, 3, 6, 9, 4, 5, -1]
print("Median of data-set is : % s "
% (statistics.median(data1)))
|
Output :
Median of data-set is : 3.5
Code #2 :
Python3
from statistics import median
from fractions import Fraction as fr
data1 = (2, 3, 4, 5, 7, 9, 11)
data2 = (2.4, 5.1, 6.7, 8.9)
data3 = (fr(1, 2), fr(44, 12),
fr(10, 3), fr(2, 3))
data4 = (-5, -1, -12, -19, -3)
data5 = (-1, -2, -3, -4, 4, 3, 2, 1)
print("Median of data-set 1 is % s" % (median(data1)))
print("Median of data-set 2 is % s" % (median(data2)))
print("Median of data-set 3 is % s" % (median(data3)))
print("Median of data-set 4 is % s" % (median(data4)))
print("Median of data-set 5 is % s" % (median(data5)))
|
Output :
Median of data-set 1 is 5
Median of data-set 2 is 5.9
Median of data-set 3 is 2
Median of data-set 4 is -5
Median of data-set 5 is 0.0
Code #3 : Demonstrating StatisticsError
Python3
from statistics import median
empty = []
print(median(empty))
|
Output :
Traceback (most recent call last):
File "/home/3c98774036f97845ee9f65f6d3571e49.py", line 12, in
print(median(empty))
File "/usr/lib/python3.5/statistics.py", line 353, in median
raise StatisticsError("no median for empty data")
statistics.StatisticsError: no median for empty data
Applications :
For practical applications, different measures of dispersion and population tendency are compared on the basis of how well the corresponding population values can be estimated. For example, a comparison shows that the sample mean is more statistically efficient than the sample median when the data is uncontaminated by data from heavily-tailed data distribution or from mixtures of data distribution, but less efficient otherwise and that the efficiency of the sample median is higher than that for a wide range of distributions. To be more specific, the median has 64% efficiency compared to minimum-variance-mean ( for large normal samples ).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...