harmonic_mean() in Python
Last Updated :
29 Sep, 2021
Harmonic Mean (also known as Contrary mean) is one of several kinds of average and in particular one of the Pythagorean means. Usually used in situations when average rates are desired. The harmonic mean is also the reciprocal of the arithmetic mean of the reciprocals of a given set of observations.
For example, harmonic mean of 1, 4 and 4 can be calculated as :
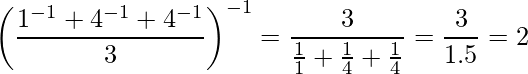
Harmonic mean can be incorporated in Python3 by using harmonic_mean() function from the statistics module.
Syntax : harmonic_mean([data-set])
Parameters :
[data-set]: which is a list or tuple or iterator of real valued numbers.
Returntype : Returns the harmonic_mean of the given set of data.
Errors and Exceptions :
StatisticsError when a empty data-set is passed or if data-set consist of negative values.
TypeError for dataset of non-numeric type values.
Note: Harmonic mean is calculated only using positive values in the list, set, or any sequence.
Code #1 :
Python3
import statistics
data = [1, 3, 5, 7, 9]
print("Harmonic Mean is % s " % (statistics.harmonic_mean(data)))
|
Output :
Harmonic Mean is 2.797513321492007
Code #2 :
Python3
from statistics import harmonic_mean
from fractions import Fraction as fr
data1 = (2, 3, 4, 5, 7, 9, 11)
data2 = (2.4, 5.1, 6.7, 8.9)
data3 = (fr(1, 2), fr(44, 12), fr(10, 3), fr(2, 3))
data4 = {1: "one", 2: "two", 3: "three"}
print("Harmonic Mean of data set 1 is % s"
% (harmonic_mean(data1)))
print("Harmonic Mean of data set 2 is % s"
% (harmonic_mean(data2)))
print("Harmonic Mean of data set 3 is % s"
% (harmonic_mean(data3)))
print("Harmonic Mean of data set 4 is % s"
% (harmonic_mean(data4)))
|
Output :
Harmonic Mean of data set 1 is 4.299197943900386
Harmonic Mean of data set 2 is 4.574783168721765
Harmonic Mean of data set 4 is 55/56
Harmonic Mean of data set 5 is 1.6363636363636365
Code #3 : Demonstrating StatisticsError
Python3
import statistics
dat1 = [1, -1]
print(statistics.harmonic_mean(dat1))
|
Output :
Traceback (most recent call last):
File "C:/Users/Souveek/PycharmProjects/Test.py", line 12, in
print(statistics.harmonic_mean((1, -1)))
File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 356, in harmonic_mean
T, total, count = _sum(1/x for x in _fail_neg(data, errmsg))
File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 148, in _sum
for n, d in map(_exact_ratio, values):
File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 356, in
T, total, count = _sum(1/x for x in _fail_neg(data, errmsg))
File "C:\Users\Souveek\AppData\Local\Programs\Python\Python36-32\Lib\statistics.py", line 285, in _fail_neg
raise StatisticsError(errmsg)
statistics.StatisticsError: harmonic mean does not support negative values
Note: Following codes may not run on online IDEs, since the harmonic_mean() function is newly introduced in Python3.6
Applications :
Harmonic Mean is one of the many important tools in finance (under statistics). The weighted harmonic mean is the preferable method for averaging multiples, such as the price–earnings ratio (P/E), in which price is in the numerator. It is also used in calculations in places where the arithmetic mean overestimates the required result.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...