Python program to Compute a Polynomial Equation
Last Updated :
21 Jun, 2022
The following article contains programs to compute a polynomial equation given that the coefficients of the polynomial are stored in a List.
Examples:
# Evaluate value of 2x3 - 6x2 + 2x - 1 for x = 3
Input: poly[] = {2, -6, 2, -1}, x = 3
Output: 5
# Evaluate value of 2x3 + 3x + 1 for x = 2
Input: poly[] = {2, 0, 3, 1}, x = 2
Output: 23
# Evaluate value of 2x + 5 for x = 5
Input: poly[] = {2, 5}, x = 5
Output: 15The equation will be of type:
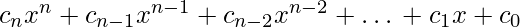
We will be provided with the value of variable and we have to compute the value of the polynomial at that point. To do so we have two approaches.
Approach
- Naive Method: Using for loop to compute the value.
- Optimised Method: Using Horner’s Method for computing the value.
Naive method:
In this approach, the following methodology will be followed. This is the most naive approach to do such questions.
- First coefficient cn will be multiplied with xn
- Then coefficient cn-1 will be multiplied with xn-1
- The results produced in the above two steps will be added
- This will go on till all the coefficient are covered.
Example:
Python3
poly = [2, -6, 2, -1]
x = 3
n = len(poly)
result = 0
for i in range(n):
Sum = poly[i]
for j in range(n - i - 1):
Sum = Sum * x
result = result + Sum
print(result)
|
Output:
5
Time Complexity: O(n2)
Optimized method:
Horner’s method can be used to evaluate polynomial in O(n) time. To understand the method, let us consider the example of 2x3 – 6x2 + 2x – 1. The polynomial can be evaluated as ((2x – 6)x + 2)x – 1. The idea is to initialize result as the coefficient of xn which is 2 in this case, repeatedly multiply the result with x and add the next coefficient to result. Finally, return the result.
Python3
def horner(poly, n, x):
result = poly[0]
for i in range(1, n):
result = result*x + poly[i]
return result
poly = [2, -6, 2, -1]
x = 3
n = len(poly)
print("Value of polynomial is:", horner(poly, n, x))
|
Output:
Value of polynomial is: 5
Time Complexity: O(n)
Share your thoughts in the comments
Please Login to comment...