Python Program for Topological Sorting
Last Updated :
28 Aug, 2023
Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge uv, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.
Python Program for Topological Sorting
For example, a topological sorting of the following graph is “5 4 2 3 1 0”. There can be more than one topological sorting for a graph. For example, another topological sorting of the following graph is “4 5 2 3 1 0”. The first vertex in topological sorting is always a vertex with in-degree as 0 (a vertex with no in-coming edges).
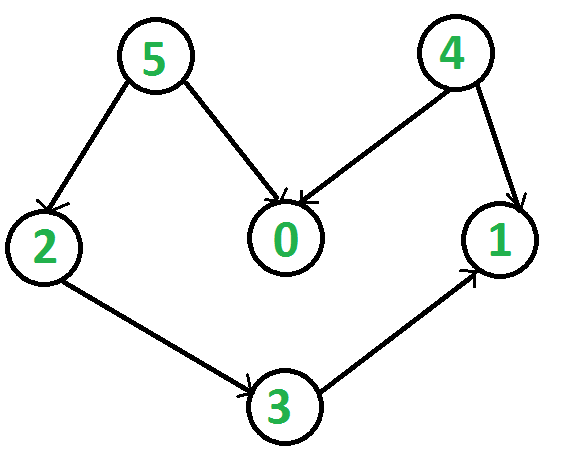
Topological sorting can be implemented recursively and non-recursively. First, we show the clearer recursive version, then provide the non-recursive version with analysis.
Recursive Topological Sorting
Python3
from collections import defaultdict
class Graph:
def __init__(self,vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def topologicalSortUtil(self,v,visited,stack):
visited[v] = True
for i in self.graph[v]:
if visited[i] == False:
self.topologicalSortUtil(i,visited,stack)
stack.insert(0,v)
def topologicalSort(self):
visited = [False]*self.V
stack =[]
for i in range(self.V):
if visited[i] == False:
self.topologicalSortUtil(i,visited,stack)
print (stack)
g= Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
print ("Following is a Topological Sort of the given graph")
g.topologicalSort()
|
Output
Following is a Topological Sort of the given graph
[5, 4, 2, 3, 1, 0]
Non-recursive Topological Sorting Python
Algorithm:
The way topological sorting is solved is by processing a node after all of its children are processed. Each time a node is processed, it is pushed onto a stack in order to save the final result. This non-recursive solution builds on the same concept of DFS with a little tweak which can be understood above and in this article. However, unlike the recursive solution, which saves the order of the nodes in the stack after all the neighboring elements have been pushed to the program stack, this solution replaces the program stack with a working stack. If a node has a neighbor that has not been visited, the current node and the neighbor are pushed to the working stack to be processed until there are no more neighbors available to be visited.
After all the nodes have been visited, what remains is the final result which is found by printing the stack result in reverse.
Python3
from collections import defaultdict
class Graph:
def __init__(self,vertices):
self.graph = defaultdict(list)
self.V = vertices
def addEdge(self,u,v):
self.graph[u].append(v)
def neighbor_gen(self,v):
for k in self.graph[v]:
yield k
def nonRecursiveTopologicalSortUtil(self, v, visited,stack):
working_stack = [(v,self.neighbor_gen(v))]
while working_stack:
v, gen = working_stack.pop()
visited[v] = True
for next_neighbor in gen:
if not visited[next_neighbor]:
working_stack.append((v,gen))
working_stack.append((next_neighbor, self.neighbor_gen(next_neighbor)))
break
else:
stack.append(v)
def nonRecursiveTopologicalSort(self):
visited = [False]*self.V
stack = []
for i in range(self.V):
if not(visited[i]):
self.nonRecursiveTopologicalSortUtil(i, visited,stack)
stack.reverse()
print(stack)
g= Graph(6)
g.addEdge(5, 2);
g.addEdge(5, 0);
g.addEdge(4, 0);
g.addEdge(4, 1);
g.addEdge(2, 3);
g.addEdge(3, 1);
print("The following is a Topological Sort of the given graph")
g.nonRecursiveTopologicalSort()
|
Output
The following is a Topological Sort of the given graph
[5, 4, 2, 3, 1, 0]
Complexity Analysis:
- Time Complexity: O(V + E): The above algorithm is simply DFS with a working stack and a result stack. Unlike the recursive solution, recursion depth is not an issue here.
- Auxiliary space: O(V): The extra space is needed for the 2 stacks used.
Please refer complete article on Topological Sorting for more details.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...