Python Program for nth Catalan Number
Last Updated :
13 Jun, 2022
Catalan numbers are a sequence of natural numbers that occurs in many interesting counting problems like the following.
1) Count the number of expressions containing n pairs of parentheses which are correctly matched. For n = 3, possible expressions are ((())), ()(()), ()()(), (())(), (()()).
2) Count the number of possible Binary Search Trees with n keys (See this)
See this for more applications.
The first few Catalan numbers for n = 0, 1, 2, 3, … are 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, …
Recursive Solution
Catalan numbers satisfy the following recursive formula.
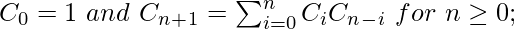
Following is the implementation of above recursive formula.
Python3
def catalan(n):
if n <= 1:
return 1
res = 0
for i in range(n):
res += catalan(i) * catalan(n-i-1)
return res
for i in range(10):
print(catalan(i), end=' ')
|
Output: 1 1 2 5 14 42 132 429 1430 4862
Time Complexity: O(2n)
Auxiliary Space: O(n)
Dynamic Programming Solution
We can observe that the above recursive implementation does a lot of repeated work (we can the same by drawing a recursion tree). Since there are overlapping sub-problems, we can use dynamic programming for this. Following is a Dynamic programming-based implementation in Python.
Python3
def catalan(n):
if (n == 0 or n == 1):
return 1
catalan = [0 for i in range(n + 1)]
catalan[0] = 1
catalan[1] = 1
for i in range(2, n + 1):
catalan[i] = 0
for j in range(i):
catalan[i] += catalan[j] * catalan[i-j-1]
return catalan[n]
for i in range(10):
print(catalan(i))
|
Output: 1
1
2
5
14
42
132
429
1430
4862
Time Complexity: O(n^2)
Auxiliary Space: O(n)
Please refer complete article on Program for nth Catalan Number for more details!
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...