Python Program for N Queen Problem | Backtracking-3
Last Updated :
31 May, 2022
The N Queen is the problem of placing N chess queens on an N×N chessboard so that no two queens attack each other. For example, the following is a solution for 4 Queen problem.
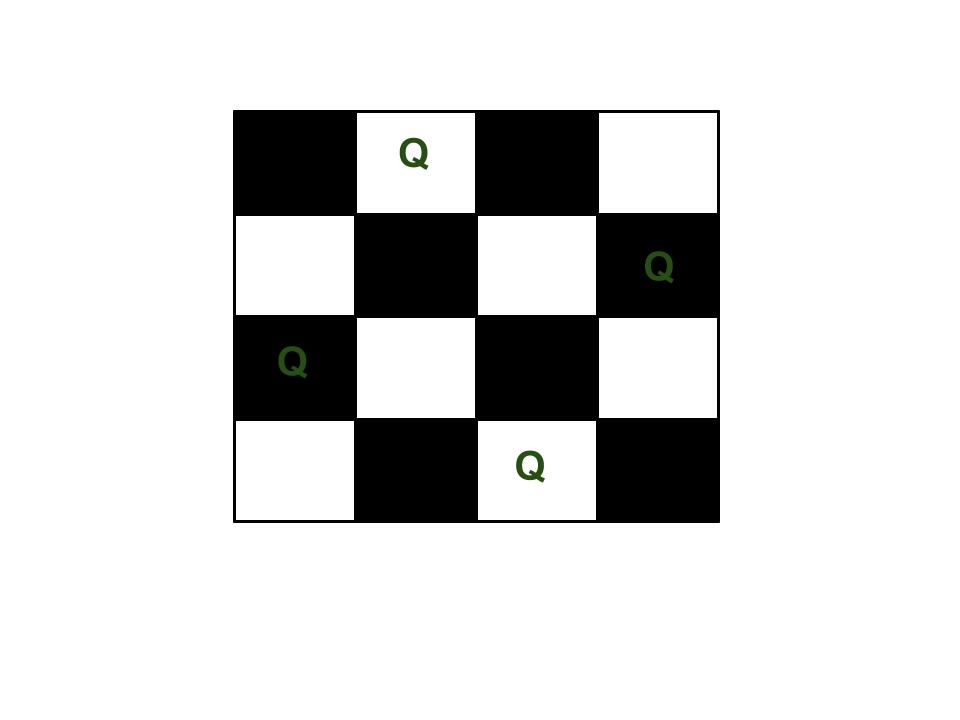
The expected output is a binary matrix that has 1s for the blocks where queens are placed. For example, the following is the output matrix for above 4 queen solution.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
Python3
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print (board[i][j],end=' ')
print()
def isSafe(board, row, col):
for i in range(col):
if board[row][i] == 1:
return False
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
for i, j in zip(range(row, N, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
if col >= N:
return True
for i in range(N):
if isSafe(board, i, col):
board[i][col] = 1
if solveNQUtil(board, col + 1) == True:
return True
board[i][col] = 0
return False
def solveNQ():
board = [ [0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
]
if solveNQUtil(board, 0) == False:
print ("Solution does not exist")
return False
printSolution(board)
return True
solveNQ()
|
Output:
0 0 1 0
1 0 0 0
0 0 0 1
0 1 0 0
Time Complexity: O(N2)
Auxiliary Space: O(N)
Please refer complete article on N Queen Problem | Backtracking-3 for more details!
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...