Python Program for Kronecker Product of two matrices
Last Updated :
25 Apr, 2022
Given a 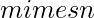 matrix A and a
matrix A and a 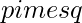 matrix B, their Kronecker product C = A tensor B, also called their matrix direct product, is an
matrix B, their Kronecker product C = A tensor B, also called their matrix direct product, is an 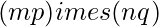 matrix.
matrix.
A tensor B = |a11B a12B|
|a21B a22B|
= |a11b11 a11b12 a12b11 a12b12|
|a11b21 a11b22 a12b21 a12b22|
|a11b31 a11b32 a12b31 a12b32|
|a21b11 a21b12 a22b11 a22b12|
|a21b21 a21b22 a22b21 a22b22|
|a21b31 a21b32 a22b31 a22b32|
Examples:
1. The matrix direct(kronecker) product of the 2×2 matrix A
and the 2×2 matrix B is given by the 4×4 matrix :
Input : A = 1 2 B = 0 5
3 4 6 7
Output : C = 0 5 0 10
6 7 12 14
0 15 0 20
18 21 24 28
2. The matrix direct(kronecker) product of the 2×3 matrix A
and the 3×2 matrix B is given by the 6×6 matrix :
Input : A = 1 2 B = 0 5 2
3 4 6 7 3
1 0
Output : C = 0 5 2 0 10 4
6 7 3 12 14 6
0 15 6 0 20 8
18 21 9 24 28 12
0 5 2 0 0 0
6 7 3 0 0 0
Below is the code to find the Kronecker Product of two matrices and stores it as matrix C :
Python3
cola = 2
rowa = 3
colb = 3
rowb = 2
def Kroneckerproduct( A , B ):
C = [[0 for j in range(cola * colb)] for i in range(rowa * rowb)]
for i in range(0, rowa):
for k in range(0, rowb):
for j in range(0, cola):
for l in range(0, colb):
C[i + l + 1][j + k + 1] = A[i][j] * B[k][l]
print (C[i + l + 1][j + k + 1],end=' ')
print ("
")
A = [[0 for j in range(2)] for i in range(3)]
B = [[0 for j in range(3)] for i in range(2)]
A[0][0] = 1
A[0][1] = 2
A[1][0] = 3
A[1][1] = 4
A[2][0] = 1
A[2][1] = 0
B[0][0] = 0
B[0][1] = 5
B[0][2] = 2
B[1][0] = 6
B[1][1] = 7
B[1][2] = 3
Kroneckerproduct( A , B )
|
Output :
0 5 2 0 10 4
6 7 3 12 14 6
0 15 6 0 20 8
18 21 9 24 28 12
0 5 2 0 0 0
6 7 3 0 0 0
Time Complexity: O(rowa*rowb*cola*colb), as we are using nested loops.
Auxiliary Space: O((rowa + colb) * (rowb + cola)), as we are not using any extra space.
Please refer complete article on Kronecker Product of two matrices for more details!
Share your thoughts in the comments
Please Login to comment...