Python Program for Finding the vertex, focus and directrix of a parabola
Last Updated :
14 Mar, 2023
A set of points on a plain surface that forms a curve such that any point on that curve is equidistant from the focus is a
parabola.
Vertex of a parabola is the coordinate from which it takes the sharpest turn whereas a is the straight line used to generate the curve.
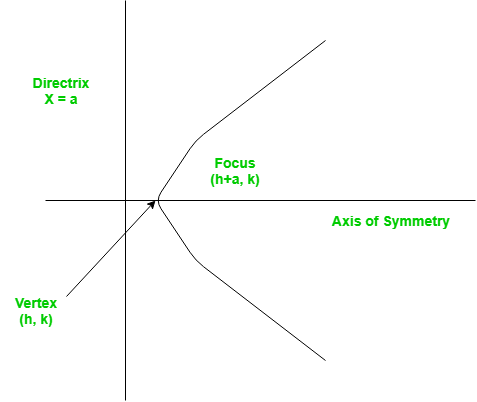
The standard form of a parabola equation is
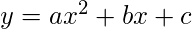
. Given the values of a, b and c; our task is to find the coordinates of vertex, focus and the equation of the directrix.
Example –
Input : 5 3 2
Output : Vertex:(-0.3, 1.55)
Focus: (-0.3, 1.6)
Directrix: y=-198
Consult the formula below for explanation.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...