Python Program For Finding Intersection Point Of Two Linked Lists
Last Updated :
17 Aug, 2023
There are two singly linked lists in a system. By some programming error, the end node of one of the linked list got linked to the second list, forming an inverted Y-shaped list. Write a program to get the point where two linked lists merge.
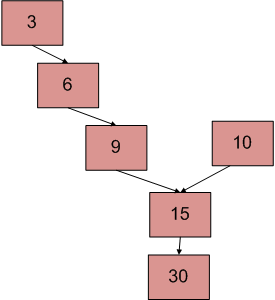
Above diagram shows an example with two linked lists having 15 as intersection points.
Method 1(Simply use two loops):
Use 2 nested for loops. The outer loop will be for each node of the 1st list and the inner loop will be for the 2nd list. In the inner loop, check if any of the nodes of the 2nd list is the same as the current node of the first linked list. The time complexity of this method will be O(M * N) where m and n are the numbers of nodes in two lists.
Method 2 (Mark Visited Nodes):
This solution requires modifications to basic linked list data structure. Have a visited flag with each node. Traverse the first linked list and keep marking visited nodes. Now traverse the second linked list, If you see a visited node again then there is an intersection point, return the intersecting node. This solution works in O(m+n) but requires additional information with each node. A variation of this solution that doesn’t require modification to the basic data structure can be implemented using a hash. Traverse the first linked list and store the addresses of visited nodes in a hash. Now traverse the second linked list and if you see an address that already exists in the hash then return the intersecting node.
Method 3(Using difference of node counts):
- Get count of the nodes in the first list, let count be c1.
- Get count of the nodes in the second list, let count be c2.
- Get the difference of counts d = abs(c1 – c2)
- Now traverse the bigger list from the first node till d nodes so that from here onwards both the lists have equal no of nodes
- Then we can traverse both the lists in parallel till we come across a common node. (Note that getting a common node is done by comparing the address of the nodes)
Below image is a dry run of the above approach:

Below is the implementation of the above approach :
Python3
class Node:
def __init__(self, data):
self.data = data
self.next = None
def getIntersectionNode(head1, head2):
c1=getCount(head1)
c2=getCount(head2)
if c1 > c2:
d = c1 - c2
return _getIntersectionNode(d, head1,
head2)
else:
d = c2 - c1
return _getIntersectionNode(d, head2,
head1)
def _getIntersectionNode(d, head1, head2):
current1 = head1
current2 = head2
for i in range(d):
if current1 is None:
return -1
current1 = current1.next
while current1 is not None and current2 is not None:
if current1 is current2:
return current1.data
current1 = current1.next
current2 = current2.next
return -1
def getCount(node):
cur=node
count=0
while cur is not None:
count+=1
cur=cur.next
return count
if __name__ == '__main__':
common = Node(15)
head1 = Node(3)
head1.next = Node(6)
head1.next.next = Node(9)
head1.next.next.next = common
head1.next.next.next.next = Node(30)
head2 = Node(10)
head2.next = common
head2.next.next = Node(30)
print("The node of intersection is ",
getIntersectionNode(head1,head2))
|
Output:
The node of intersection is 15
Time Complexity: O(m+n)
Auxiliary Space: O(1)
Method 4(Make circle in first list):
Thanks to Saravanan Man for providing below solution.
1. Traverse the first linked list(count the elements) and make a circular linked list. (Remember the last node so that we can break the circle later on).
2. Now view the problem as finding the loop in the second linked list. So the problem is solved.
3. Since we already know the length of the loop(size of the first linked list) we can traverse those many numbers of nodes in the second list, and then start another pointer from the beginning of the second list. we have to traverse until they are equal, and that is the required intersection point.
4. remove the circle from the linked list.
Time Complexity: O(m+n)
Auxiliary Space: O(1)
Method 5 (Reverse the first list and make equations):
Thanks to Saravanan Mani for providing this method.
1) Let X be the length of the first linked list until intersection point.
Let Y be the length of the second linked list until the intersection point.
Let Z be the length of the linked list from the intersection point to End of
the linked list including the intersection node.
We Have
X + Z = C1;
Y + Z = C2;
2) Reverse first linked list.
3) Traverse Second linked list. Let C3 be the length of second list - 1.
Now we have
X + Y = C3
We have 3 linear equations. By solving them, we get
X = (C1 + C3 – C2)/2;
Y = (C2 + C3 – C1)/2;
Z = (C1 + C2 – C3)/2;
WE GOT THE INTERSECTION POINT.
4) Reverse first linked list.
Advantage: No Comparison of pointers.
Disadvantage: Modifying linked list(Reversing list).
Time complexity: O(m+n)
Auxiliary Space: O(1)
Method 6 (Traverse both lists and compare addresses of last nodes): This method is only to detect if there is an intersection point or not. (Thanks to NeoTheSaviour for suggesting this)
1) Traverse list 1, store the last node address
2) Traverse list 2, store the last node address.
3) If nodes stored in 1 and 2 are same then they are intersecting.
The time complexity of this method is O(m+n) and used Auxiliary space is O(1)
Please refer complete article on Write a function to get the intersection point of two Linked Lists for more details!
Share your thoughts in the comments
Please Login to comment...