Python Program for Diagonally Dominant Matrix

In mathematics, a square matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other (non-diagonal) entries in that row. More precisely, the matrix A is diagonally dominant if 

For example, The matrix 

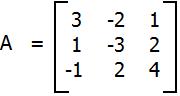
is diagonally dominant because 
|a₁₁| ? |a₁₂| + |a₁₃| since |+3| ? |-2| + |+1| 
|a₂₂| ? |a₂₁| + |a₂₃| since |-3| ? |+1| + |+2| 
|a₃₃| ? |a₃₁| + |a₃₂| since |+4| ? |-1| + |+2|
Given a matrix A of n rows and n columns. The task is to check whether matrix A is diagonally dominant or not.
Examples :

Input : A = { { 3, -2, 1 },
              { 1, -3, 2 },
              { -1, 2, 4 } };
Output : YES
Given matrix is diagonally dominant
because absolute value of every diagonal
element is more than sum of absolute values
of corresponding row.

Input : A = { { -2, 2, 1 },
              { 1, 3, 2 },
              { 1, -2, 0 } };
Output : NO

The idea is to run a loop from i = 0 to n-1 for the number of rows and for each row, run a loop j = 0 to n-1 find the sum of non-diagonal element i.e i != j. And check if diagonal element is greater than or equal to sum. If for any row, it is false, then return false or print “No”. Else print “YES”. 

Python3

# Python Program to check
# whether given matrix is
# Diagonally Dominant Matrix.

# check the given
# matrix is Diagonally
# Dominant Matrix or not.
def isDDM(m, n) :

    # for each row
    for i in range(0, n) :

        # for each column, finding
        # sum of each row.
        sum = 0
        for j in range(0, n) :
            sum = sum + abs(m[i][j])

        # removing the
        # diagonal element.
        sum = sum - abs(m[i][i])

        # checking if diagonal
        # element is less than
        # sum of non-diagonal
        # element.
        if (abs(m[i][i]) < sum) :
            return False

    return True

# Driver Code
n = 3
m = [[ 3, -2, 1 ],
    [ 1, -3, 2 ],
    [ -1, 2, 4 ]]

if((isDDM(m, n))) :
    print ("YES")
else :
    print ("NO")

# This code is contributed by
# Manish Shaw(manishshaw1)

Output :

YES

Time Complexity: O(N²)

Auxiliary Space: O(1)

Please refer complete article on Diagonally Dominant Matrix for more details!