Python Program for Breadth First Search or BFS for a Graph

Breadth First Traversal (or Search)

for a graph is similar to Breadth First Traversal of a tree (See method 2 of

this post

).

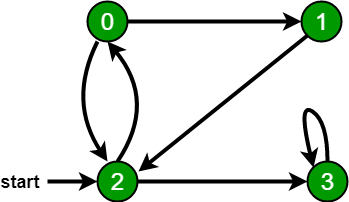
The only catch here is, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we use a boolean visited array. For simplicity, it is assumed that all vertices are reachable from the starting vertex. For example, in the following graph, we start traversal from vertex 2. When we come to vertex 0, we look for all adjacent vertices of it. 2 is also an adjacent vertex of 0. If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process. A Breadth First Traversal of the following graph is 2, 0, 3, 1.

Following are the implementations of simple Breadth First Traversal from a given source. The implementation uses

adjacency list representation

of graphs.

STL

\’s

list container

is used to store lists of adjacent nodes and queue of nodes needed for BFS traversal.

Python3

# Python3 Program to print BFS traversal
# from a given source vertex. BFS(int s)
# traverses vertices reachable from s.

from collections import defaultdict


# This class represents a directed graph
# using adjacency list representation
class Graph:

    # Constructor
    def __init__(self):

        # Default dictionary to store graph
        self.graph = defaultdict(list)

    # Function to add an edge to graph
    def addEdge(self, u, v):
        self.graph[u].append(v)

    # Function to print a BFS of graph
    def BFS(self, s):

        # Mark all the vertices as not visited
        visited = [False] * (max(self.graph) + 1)

        # Create a queue for BFS
        queue = []

        # Mark the source node as
        # visited and enqueue it
        queue.append(s)
        visited[s] = True

        while queue:

            # Dequeue a vertex from
            # queue and print it
            s = queue.pop(0)
            print(s, end=" ")

            # Get all adjacent vertices of the
            # dequeued vertex s.
            # If an adjacent has not been visited,
            # then mark it visited and enqueue it
            for i in self.graph[s]:
                if visited[i] == False:
                    queue.append(i)
                    visited[i] = True


# Driver code
if __name__ == '__main__':

    # Create a graph given in
    # the above diagram
    g = Graph()
    g.addEdge(0, 1)
    g.addEdge(0, 2)
    g.addEdge(1, 2)
    g.addEdge(2, 0)
    g.addEdge(2, 3)
    g.addEdge(3, 3)

    print("Following is Breadth First Traversal"
        " (starting from vertex 2)")
    g.BFS(2)

# This code is contributed by Neelam Yadav

Output

Following is Breadth First Traversal (starting from vertex 2)
2 0 3 1 

Time Complexity

: O(V+E) where V is the number of vertices in graph and E is the number of edges

Auxiliary Space

: O(V) Please refer complete article on

Breadth First Search or BFS for a Graph

for more details!