Python | Percentage increase in hemisphere volume if radius is increased

Given that the radius of a hemisphere is increased by a fixed percentage so, the target is to calculate the percentage increase in the volume of the hemisphere.

Examples:
Input :
20
Output :
72.8 %
Input :
70
Output :
391.3 %

Approach:
Let, the radius of the hemisphere = 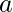$a$
Given percentage increase = 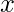$x%$
Volume before increase = 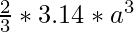$\frac{2}{3} * 3.14*a^3$
New radius after increase = 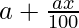$a + \frac{ax}{100}$
So, new volume = 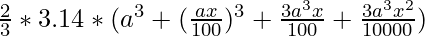$\frac{2}{3}*3.14*(a^3 + (\frac{ax}{100})^3 + \frac{3a^3x}{100} + \frac{3a^3x^2}{10000})$
Change in volume = 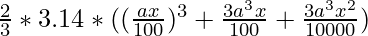$\frac{2}{3}*3.14*((\frac{ax}{100})^3 + \frac{3a^3x}{100} + \frac{3a^3x^2}{10000})$
Percentage increase in volume = $(\frac{2}{3}*3.14*((\frac{ax}{100})^3 + \frac{3a^3x}{100} + \frac{3a^3x^2}{10000})/\frac{2}{3}*3.14*a^3) * 100 = \frac{x^3}{10000} + 3x + \frac{3x^2}{100}$
Below is the Python code implementation of the above mentioned approach.

Python3

# Python3 program to find percentage increase
# in the volume of the hemisphere
# if the radius is increased by a given percentage
   
def newvol(x):
   
    print('percentage increase in the  volume of the hemisphere is ', pow(x, 3) / 10000 + 3 * x
                + (3 * pow(x, 2)) / 100, '%')
   
# Driver code
x = 10.0
newvol(x)

Output :

percentage increase in the volume of the hemisphere is  33.1 %

Time Complexity: O(log x) because pow function would take logarithmic time

Auxiliary Space: O(1)

Recommended

Solve DSA problems on GfG Practice.

Solve Problems

Last Updated : 20 Feb, 2023

Python | Percentage increase in hemisphere volume if radius is increased

Python3

Please Login to comment...